Correlation structure of nested nonlinear mixed model

Question

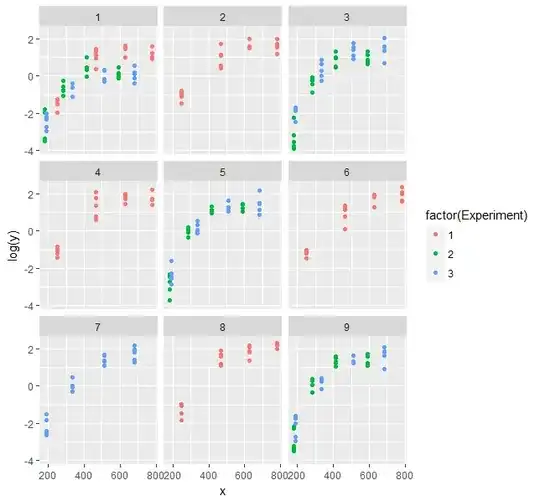
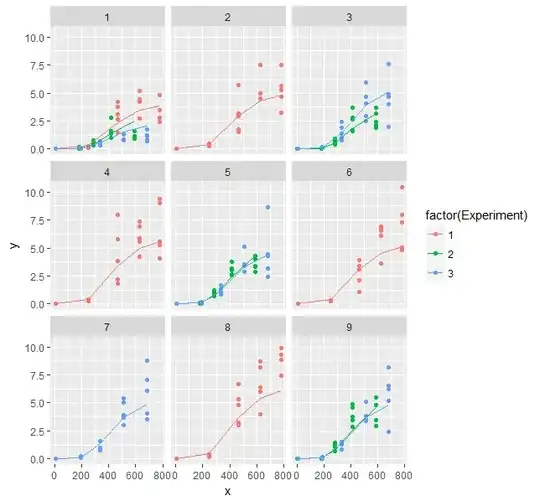
I would appreciate any help. I am trying to fit a nonlinear mixed model to some experiments. I have adopted a Gompertz function (y=Asym*exp(-b2*b3^x)), and the data used is 3 years of experiments (the doses were not always the same and I removed some outliers before any analysis). Moreover, since the measurements were destructive, it is not a repeated measure case. I am fitting a nested model in R (nlme package, tried with lme4 as well). The data are here. The final model adopted by now is:

model <- nlme(y ~ SSgompertz(x,Asym,b2,b3),
              data = Data,
              fixed = Asym + b2 + b3 ~ 1,
              random = Asym ~ 1|Experiment/Treatment,
              start = c(Asym = 5, b2 = 30, b3 = 0.8), 
              verbose = T, na.action = na.omit, method="ML",
              control = nlmeControl(maxIter=100000, opt="nlminb", pnlsTol=0.01)) 

In relation to diagnosis plots:

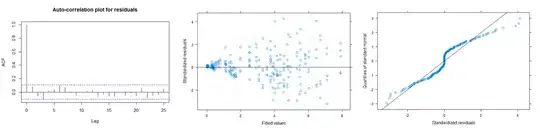
1. There does not seem to be a normality problem.
2. There isn't a problem with autocorrelation. However, if I can include an autocorrelation structure between groups, I think the model can be improved.
3. There is increasing variability. So including a heterogeneous variance for the error term will improve the model and will help to deal with the heteroscedasticity.

The summary of the model gives a high negative correlation between b2 and b3 parameters. I am not sure how bad is this.

So my questions is: How can I correctly specify a correlation structure? I have been trying different ways and methods for the correlation function without success. On the other hand, the inclusion of weights and more random effects did not improve the model. I was planning to include a covariate but this option has not been implemented for nested models in nlme. So, in addition to specifying a correlation structure, how could I improve the model's results?

Answer 1

Disclaimer: In the following I'll assume that your random structure is correct. I cannot judge that without more information and it would be beyond the scope of one question anyway.

Let's plot your data:

library(ggplot2)
ggplot(Data, aes(x = x, y = y, color = factor(Experiment))) +
  geom_point() +
  facet_wrap(~ Treatmen)

What we see there is increasing scatter with increasing x-values. That's what you see as heterogeneity from your model too. You don't need a correlation structure, but need to consider the structure of the variance. You could add a variance structure to your model, but then fitting the model becomes difficult and computationally expensive. I couldn't manage a successful and reasonable fit.

The obvious alternative would be fitting a model on the log scale. However, there is a problem with your data:

summary(Data$y)
#    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
# 0.00000  0.06545  0.99720  2.12000  3.59700 10.39000 

You have exact zero values in your data. A Gompertz function does not give exact zeros. That's the limit for x going to minus infinity. Since these values were probably measured, I assume they were below the detection limit. That's not the same as zero. Thus, I'd exclude them from analysis.

Data2 <- Data[Data$y > 0,]
ggplot(Data2, aes(x = x, y = log(y), color = factor(Experiment))) +
  geom_point() +
  facet_wrap(~ Treatmen)

That looks better.

Now, the Gompertz function is:

$y = A \cdot \exp{(-\beta_2 \cdot \beta_3^x)}$

On the log-scale:

$\ln{y} = \alpha - \beta_2 \cdot \beta_3^x$

Let's fit that (you need to adjust the starting values, the estimates from the original model are helpful here):

mod2 <- nlme(log(y) ~ a - b2 * b3^x,
             data = Data2,
             fixed = a + b2 + b3 ~ 1,
             random = a ~ 1|Experiment/Treatmen,
             start = c(a = log(5), b2 = 15, b3 = 0.995), 
             verbose = T, na.action = na.omit, method="ML",
             control = nlmeControl(maxIter=100, opt="nlminb", pnlsTol=0.01))

plot(mod2)

Back-transform coefficient for asymptote:

coefs <- coef(mod2)
coefs$Asym <- exp(coefs$a)
#            a     b2        b3     Asym
#1/1 1.4106169 15.722 0.9928132 4.098483
#1/2 1.6317404 15.722 0.9928132 5.112765
#1/4 1.7736012 15.722 0.9928132 5.892034
#1/6 1.6848617 15.722 0.9928132 5.391705
#1/8 1.8593160 15.722 0.9928132 6.419344
#2/1 1.1390170 15.722 0.9928132 3.123696
#2/3 1.3801606 15.722 0.9928132 3.975540
#2/5 1.6804342 15.722 0.9928132 5.367886
#2/9 1.7479048 15.722 0.9928132 5.742558
#3/1 0.8431604 15.722 0.9928132 2.323699
#3/3 1.7521368 15.722 0.9928132 5.766912
#3/5 1.5909919 15.722 0.9928132 4.908616
#3/7 1.6985093 15.722 0.9928132 5.465793
#3/9 1.6921572 15.722 0.9928132 5.431184

Data$pred <- exp(predict(mod2, newdata = Data))

ggplot(Data, aes(x = x, y = y, color = factor(Experiment))) +
  geom_point() +
  geom_line(aes(y = pred)) +
  facet_wrap(~ Treatmen)

Regarding the high correlation between parameters: There is nothing you can do about that other than using a model with less parameters, getting more data or determining parameters independently in additional experiments. Sometimes re-parameterization of the model can help too.