20

If we want to visibly see the distribution of a continuous data, which one among histogram and pdf should be used?

What are the differences, not formula wise, between histogram and pdf?

csgillespie
  • 11,849
  • 9
  • 56
  • 85
  • Could you please clarify whether this question concerns data (whose distribution could be represented by a histogram) or theoretical constructs (such as a pdf, which describes a probability distribution). – whuber Sep 11 '10 at 21:42
  • 4
    But where does the pdf come from? By definition, a pdf describes a theoretical probability distribution. Do you perhaps mean the edf (empirical distribution function)? – whuber Sep 11 '10 at 22:38

4 Answers4

24

To clarify Dirks point :

Say your data is a sample of a normal distribution. You could construct the following plot:

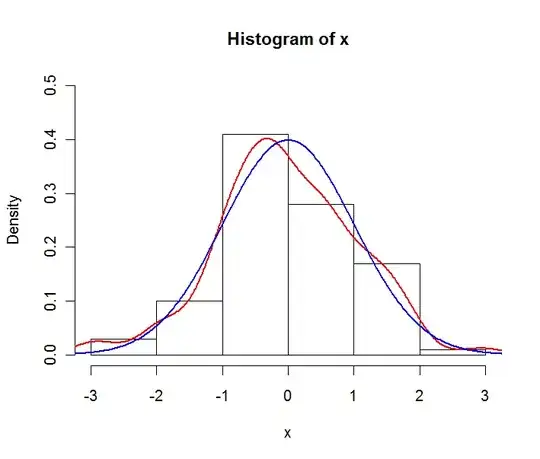
alt text

The red line is the empirical density estimate, the blue line is the theoretical pdf of the underlying normal distribution. Note that the histogram is expressed in densities and not in frequencies here. This is done for plotting purposes, in general frequencies are used in histograms.

So to answer your question : you use the empirical distribution (i.e. the histogram) if you want to describe your sample, and the pdf if you want to describe the hypothesized underlying distribution.

Plot is generated by following code in R :

x <- rnorm(100)
y <- seq(-4,4,length.out=200)

hist(x,freq=F,ylim=c(0,0.5))
lines(density(x),col="red",lwd=2)
lines(y,dnorm(y),col="blue",lwd=2)
Joris Meys
  • 5,475
  • 2
  • 32
  • 43
  • whats the difference between frequency and density? – Lakshay Jun 30 '18 at 09:28
  • 2
    @Lakshay frequency are counts. All frequencies summed equals the number of observations. Density is short for PDF (probability density function), which is a proxy for the probability of having a certain value. The area under the PDF sums to 1. – Joris Meys Jul 04 '18 at 12:37
13

A histogram is pre-computer age estimate of a density. A density estimate is an alternative.

These days we use both, and there is a rich literature about which defaults one should use.

A pdf, on the other hand, is a closed-form expression for a given distribution. That is different from describing your dataset with an estimated density or histogram.

Dirk Eddelbuettel
  • 8,362
  • 2
  • 28
  • 43
  • 1
    @Harpreet You are not estimating the shape of the PDF since as @Dirk indicated it has closed form, you just specify its parameters (e.g. $\mu$ and $\sigma^2$ for a gaussian). It will not necessarily "fit" the data. Now, there exist several kind of non-parametric density estimates, where you only use the data at hand (plus some kernel specifications or window span, etc.); see e.g., online help for the `density` R function. – chl Sep 11 '10 at 19:57
  • @Harpreet This is just Markdown syntax, as for editing a post through the online editor: `*ab*` gives *ab* (italic) `**ab**` gives **ab** (bold) `$\sqrt{2}$`=$\sqrt{2}$ – chl Sep 12 '10 at 08:00
6

There's no hard and fast rule here. If you know the density of your population, then a PDF is better. On the other hand, often we deal with samples and a histogram might convey some information that an estimated density covers up. For example, Andrew Gelman makes this point:

Variations on the histogram

A key benefit of a histogram is that, as a plot of raw data, it contains the seeds of its own error assessment. Or, to put it another way, the jaggedness of a slightly undersmoothed histogram performs a useful service by visually indicating sampling variability. That's why, if you look at the histograms in my books and published articles, I just about always use lots of bins. I also almost never like those kernel density estimates that people sometimes use to display one-dimensional distributions. I'd rather see the histogram and know where the data are.

Community
  • 1
ars
  • 12,160
  • 1
  • 36
  • 54
  • 3
    I must admit I never fully understand why Gelman advocates the use of histogram with small bin width; why not using stripchart plot or raw data with superimposed kernel density estimates, which much better convey the empirical distribution of the observed data? – chl Sep 11 '10 at 20:06
  • 2
    @chl: There are of course other good visualization methods to get a sense of sampling variability. But on the narrower comparison of histogram v. pdf under discussion here, I think his point is well made. – ars Sep 11 '10 at 20:18
  • 1
    that is a nice link, as are the papers discussed there. But, does this approach hold for simulations, in which case we are actually trying to estimate a density? – David LeBauer Mar 30 '11 at 21:41
1

Relative frequency histogram (discrete)

  • 'y' axis is Normalized count
  • 'y' axis is discrete probability for that particular bin/range
  • Normalized counts sum up to 1

Density Histogram (discrete)

  • 'y' axis is density value ( 'Normalized count' divided by 'bin width')
  • Bar areas sum to 1

Probability Density Function PDF (continuous)

  • PDF is a continuous version of a histogram since histogram bins are discrete
  • total area under Curve integrates to 1

These references were helpful :) http://stattrek.com/statistics/dictionary.aspx?definition=Probability_density_function

Continuous_probability_distribution from the above site

http://www.geog.ucsb.edu/~joel/g210_w07/lecture_notes/lect04/oh07_04_1.html

Harsha Manjunath
  • 111
  • 3