2

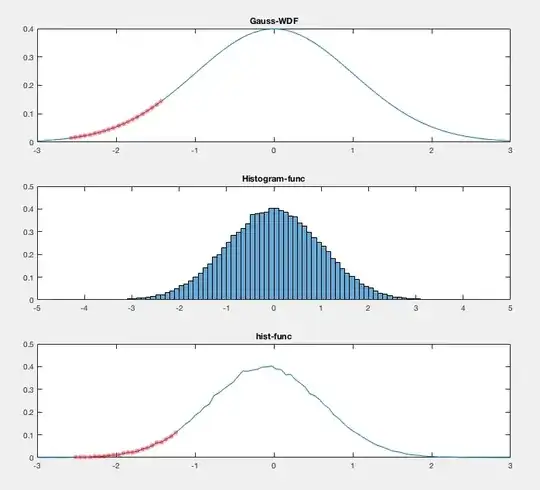
I don't understand why there is a difference between the pdf and the normalized histogram (based on randn) I plotted in matlab. Especially from -2 to -3 the difference is huge.

enter image description here

Why is the normalized histogram so far of from the ideal pdf?

Here is my code: 

q = [-3:6/99:3]; % x-Axis
f_q = (1/sqrt(2*pi*1))*exp(-0.5*((q-0)/1).^2); % Gauss pdf

n_in = 100;
y = randn(1,10000);
[n x] = hist(y,n_in); % hist func
n_norm = (n ./length(y)) ./(x(2)-x(1)); % normalize hist func
figure;
subplot(3,1,1);
plot(q,f_q);
title('Gauss-WDF')

subplot(3,1,2);
histogram(y,'Normalization', 'pdf');
title('Histogram-func');

subplot(3,1,3);
plot(q,n_norm);
title('hist-func');

EDIT:

Plot with exually distributed axis.
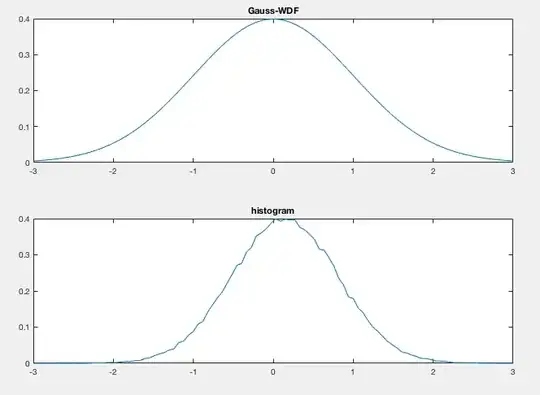
enter image description here

The histogram is based on a normal distributed random function. So it should follow the pdf of a normal distribution. But apparently it doesn't as you can obviously see. I don't understand why.

Peter
  • 23
  • 1
  • 5
  • I don't think there is a real difference. Note that all three curves have different scales. The first two differ on the x and y axes while the second and third differ only on the y-axis. – Michael R. Chernick Dec 31 '16 at 13:42
  • I meant to say that the second and third differ only on the x-axis. – Michael R. Chernick Dec 31 '16 at 13:48
  • I just checked. 1. plot: (-2/0.05) 3. plot: (-2/0.0005). So there definitely is a difference. – Peter Dec 31 '16 at 14:52
  • @Jan Can you provide your plots with equal scales i.e. where each plot has the same range of values for each axis? – epp Dec 31 '16 at 15:22
  • Exactly what "differences" do you note and how do you measure them? It's not enough just to point to wiggles in a plot: after all, your histogram describes *random* values, so *of course* they won't exactly follow a Normal curve. – whuber Dec 31 '16 at 15:23
  • I don't see any place in your code that normalizes the data. Where you write "% normalize hist func" you are doing something that differs from what "normalize" usually means. There appears to be no reason, then, to expect your histogram to agree with a *standard* Normal curve: it must be some rescaled, recentered version, up to random error. (The recentering is not visually obvious because it's so small.) – whuber Dec 31 '16 at 15:53
  • you must calculate area under histogram graphic. and than divide all frequencies to area value. and plot the results. dont forget area under pdf must be equal to 1. :) – rty Sep 30 '19 at 22:39

1 Answers1

6

If you look carefully, plots 1 and 2 are essentially the same. You've plotted them on different axes, which obfuscates things, but the probability densities at the peaks are essentially identical (roughly 0.4), and the tails of the distributions are roughly the same.

Now, it should be obvious that a pdf and a histogram won't match exactly, since the pdf is an exact expression for the probability density, and a normalized histogram is an empirical distribution formed by sampling the pdf a finite number of times (in your case, 10000). For more details, see this excellent answer

You are correct that plot 3 is different from plots 1 and 2. But that's because you attempted to write your own code for normalizing the histogram instead of using the built-in function (as you did in plot 2), and your code has a bug!

The first line of your code constructs a vector q that goes from -3 to 3. The MATLAB function hist returns bin centers as well as bin counts. In your case, the bin centers are x, and the bin counts are n. After normalizing, n becomes n_norm. When you plot the histogram, you should plot n_norm against x. Instead, you plot n_norm against q. The problem is that x ends up spanning a much larger range than q, since it extends from the smallest number you sample from randn to the largest. (And, 0.3% of values will fall outside the range -3 to 3 for a unit normal.)

When I fix this bug, all three plots look basically the same, except for the jaggedness/wiggles that is inherent to empirical distributions.

So, the lesson is: don't reinvent the wheel. ;-)

Community
  • 1
vbox
  • 586
  • 2
  • 4