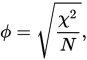7

There are several measures of association (or contingency or correlation) between two binary random variables $X$ and $Y$, among others

I wonder how the following number $\kappa$ relates to known measures, if it is statistically interesting, and under which name it is (possibly) discussed:

$$\kappa = 1 - \frac{2}{N}|X \triangle Y|$$

with $|X \triangle Y|$ the number of samples having property $X$ or property $Y$ but not both (exclusive OR, symmetric difference), $N$ the total number of samples. Like the phi coefficient, $\kappa = ± 1$ indicates perfect agreement or disagreement, and $\kappa = 0$ indicates no relationship

ttnphns
  • 51,648
  • 40
  • 253
  • 462
Hans-Peter Stricker
  • 69
  • 1
  • 11

2 Answers2

10

Using a,b,c,d convention of the 4-fold table, as here,

               Y
             1   0
            -------
        1  | a | b |
     X      -------
        0  | c | d |
            -------
a = number of cases on which both X and Y are 1
b = number of cases where X is 1 and Y is 0
c = number of cases where X is 0 and Y is 1
d = number of cases where X and Y are 0
a+b+c+d = n, the number of cases.

substitute and get

$1-\frac{2(b+c)}{n} = \frac{n-2b-2c}{n} = \frac{(a+d)-(b+c)}{a+b+c+d}$ = Hamann similarity coefficient. Meet it e.g. here. To cite:

Hamann similarity measure. This measure gives the probability that a characteristic has the same state in both items (present in both or absent from both) minus the probability that a characteristic has different states in the two items (present in one and absent from the other). HAMANN has a range of −1 to +1 and is monotonically related to Simple Matching similarity (SM), Sokal & Sneath similarity 1 (SS1), and Rogers & Tanimoto similarity (RT).

You might want to compare the Hamann formula with that of phi correlation (that you mention) given in a,b,c,d terms. Both are "correlation" measures - ranging from -1 to 1. But look, Phi's numerator $ad-bc$ will approach 1 only when both a and d are large (or likewise -1, if both b and c are large): product, you know... In other words, Pearson correlation, and especially its dichotomous-data hypostasis, Phi, is sensitive to the symmetry of marginal distributions in the data. Hamann's numerator $(a+d)-(b+c)$, having sums in place of products, is not sensitive to it: either of two summands in a pair being large is enough for the coefficient to attain close to 1 (or -1). Thus, if you want a "correlation" (or quasi-correlation) measure defying marginal distributions shape - choose Hamann over Phi.

Illustration:

Crosstabulations:
        Y
X    7     1
     1     7
Phi = .75; Hamann = .75

        Y
X    4     1
     1    10
Phi = .71; Hamann = .75
Community
  • 1
ttnphns
  • 51,648
  • 40
  • 253
  • 462
  • Is Hamann similarity widely known and accepted as an interesting measure? – Hans-Peter Stricker Jan 16 '17 at 19:42
  • 1
    How can I answer? How much widely/accepted will suffice? :-) It is sure less known than phi correlation or Jaccard similarity. Still, it is sometimes used. Google it to see... One its important property is that it is _monotonical_ equivalent of... (see the citation). – ttnphns Jan 16 '17 at 19:47
  • Sorry for my naive question, and thanks for your informative answer:-) – Hans-Peter Stricker Jan 16 '17 at 19:51
  • Can you give me a hint, under which typical circumstances I might want a "correlation defying marginal distributions shape" and choose Hamann, and under which circumstances I might want a "correlation NOT defying marginal distributions shape" and choose Phi? – Hans-Peter Stricker Jan 17 '17 at 09:56
  • Hans, if you are speaking about scientific fields or aims where we might want to use one over the other - why not ask that as a separate question? Because more people might come to answer. – ttnphns Jan 17 '17 at 17:39
4

Hubalek, Z. Coefficients of association and similarity, based on binary (presence-absence) data: an evaluation (Biol. Rev., 1982) reviews and ranks 42 different correlation coefficients for binary data. Only 3 of them meet basic statistical desiderata. Unfortunately, the issue of PRE (proportionate reduction of error) interpretation is not discussed. For the following contingency table:

        present  absent

present    a       b

absent     c       d

the association measure $r$ should meet the following obligatory conditions:

  1. $r(J,K) \le r(J,J) \quad\forall J, K$

  2. $\min(r)$ should be at $a = d = 0$ and $\max(r)$ at $b = c = 0$

  3. $r(J,K) = r(K,J) \quad \forall K,J$

  4. discrimination between positive and negative association

  5. $r$ should be linear with $\sqrt{\chi^2}$ for both subsets $ad-bc < 0 $ and $ad-bc >= 0$ (note that $\chi^2$ violates condition 4)

and ideally the following non-obligatory:

  • range of $r$ should be either $\left\{ -1 \dots +1 \right\}$, $\left\{0 \dots +1 \right\}$, or $\left\{0 \dots \infty \right\}$

  • $r(b=c=0) > r(b = 0 \veebar c = 0)$

  • $r(a=0) = min(r)$ (stricter than 2) above)

  • $r(a+1)-r(a) = r(a+2)-r(a+1)$

  • $r(a=0,b,c,d), r(a=1,b-1,c-1,d+1), r(a=2,b-2,c-2,d+2)\ldots$ should be smooth

  • homogeneous distribution of $r$ in permutation sample

  • random samples from population with known $a,b,c,d$: $r$ should show little variability even in small samples

  • simplicity of calculation, low computer time

All conditions are met by Jaccard $\left( \frac{a}{a+b+c} \right)$, Russel & Rao $\left( \frac{a} {a+b+c+d} \right)$ (both range $\left\{0 \dots +1 \right\}$) and McConnaughey $\left( \frac{a^2 - bc}{(a+b) \times (a+c)}\right)$ (range $\left\{ -1 \dots +1 \right\}$)

gibbone
  • 105
  • 2
Engelbert Buxbaum
  • 151
  • 2
  • 6