1

This question extends from two separate questions for an assignment, namely question 1 and question 2. I apologize for asking variations of questions for the same problem, but I am experiencing confusion consolidating the concepts of ANOVA.

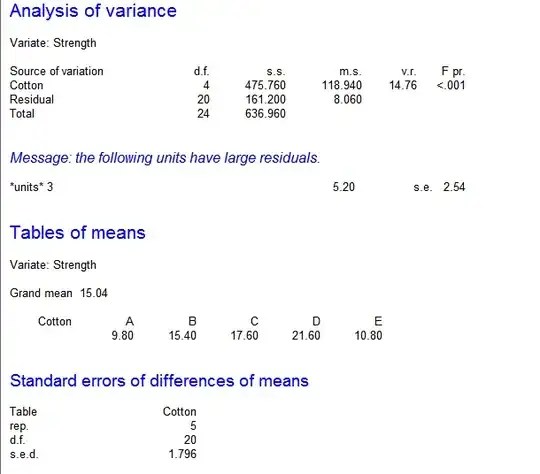
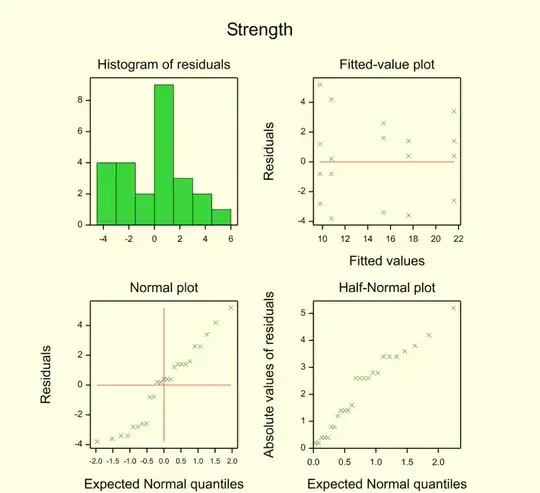
After carrying out an ANOVA, I produced a table showing the analysis of variance and associated residual plots (below). A Cross Validated question on ANOVA lists three assumptions, namely:-

  1. Independence of cases – this is an assumption of the model that simplifies the statistical analysis.

  2. Normality – the distributions of the residuals are normal.

  3. Equality (or "homogeneity") of variances, called homoscedasticity

Point of interest here what steps can be taken to check assumptions 1 and 3 by reviewing both the analysis of variance table and the residual plots (found below). I feel confident checking whether the data is normally distributed but not for homoscedasticity and independence.

The data is derived from:-

enter image description here

R Format of the Data

structure(list(Percentage_Cotton = c(15, 20, 25, 30, 35), A = c(7, 
12, 14, 19, 7), B = c(7, 17, 18, 25, 10), C = c(15, 12, 18, 22, 
11), D = c(11, 18, 19, 19, 15), E = c(9, 18, 19, 23, 11)), .Names =     c("Percentage_Cotton", 
"A", "B", "C", "D", "E"), row.names = c(NA, -5L), class = "data.frame")

Problems to solve

  1. Does the average strength of the cloth vary with the cotton percentage? I am assuming the average strength is the grand mean of 15.04

  2. Do the ANOVA assumptions appear to be in doubt? If so, what would be the most effective way to further check the assumptions required for the ANOVA to highlight existent doubts by reviewing the analysis of variance table and the residual plots?

Analysis of Variance Table

enter image description here

Residual Plots

enter image description here

Community
  • 1
Alice Hobbs
  • 273
  • 1
  • 7
  • 2
    Minimally you should cross-reference your earlier questions such as http://stats.stackexchange.com/questions/255863/help-is-the-variance-the-same-for-each-factor-level Asking small variations on the same question is not in general a good idea. – Nick Cox Jan 13 '17 at 11:24
  • 1
    http://stats.stackexchange.com/questions/254801/should-the-response-variable-meet-the-assumption-of-constant-variance is another. – Nick Cox Jan 13 '17 at 11:35
  • Hi Nick, I cross referenced the earlier questions like you suggested. I apologize for asking variations of the same question; however; this question for my assignment consists of five parts. The Cross Validated community has been wonderful because I am still experiencing confusion regarding the theory of ANOVA and how to check associated assumptions. I am double guessing myself and I just want to make sure that I am understanding the theory correctly from different perspectives, which will be invaluable in the future. Many thanks in advance, your assistance has been deeply appreciated. – Alice Hobbs Jan 13 '17 at 18:01
  • OK. My personal position is that this question the graphs say nothing about independence; that is, or is not, a feature of the design. The previous thread dealt with the question of thinking about homo- and heteroscedasticity, so I struggle to find a new, answerable question here. I think your sources are overstating the need for normal distributions, by the way. – Nick Cox Jan 13 '17 at 18:14
  • I agree, the data is definitely not normal. – Alice Hobbs Jan 13 '17 at 18:15
  • That's not what I said or meant; in fact the distribution of residuals looks quite well behaved here for a small sample. My point: I don't think that the assumption of normality is an important as listing it second implies. For more, see e.g. Miller, _Beyond ANOVA_. – Nick Cox Jan 13 '17 at 18:19

0 Answers0