12

I have a sample of data generated in R by rnorm(50,0,1), so the data obviously takes on a normal distribution. However, R doesn't "know" this distributional information about the data.

Is there a method in R that can estimate what kind of distribution my sample comes from? If not, I will use the shapiro.test function and proceed that way.

cardinal
  • 24,973
  • 8
  • 94
  • 128
James Highbright
  • 149
  • 1
  • 1
  • 7
  • I'm not sure I recognize the upshot of this question. It is true that if you just have a vector of numbers in R, there isn't a lot of metadata associated with it, but why would that bother you? Why would you need that / what would you want to do with it? Suppose it did have such, it would only be helpful to the extent that you were to pass that vector to a function with specific methods for Gaussian data vs. other. I don't know of any (although I'm hardly the world's most expert R user). – gung - Reinstate Monica Mar 30 '12 at 22:42
  • If you just want to test whether any given sample seems normal, the Shapiro-Wilk test is a decent option (although it's worth your while to read [this question](http://stats.stackexchange.com/questions/2492/) and the answers given there). I can see how this could come up in a simulation study, but without more details about the study, it's hard to give a useful answer. – gung - Reinstate Monica Mar 30 '12 at 22:43
  • Why do you need to identify a distribution for the data? Automatic distributional choice is often an attractive idea, but that doesn't make it a good idea. – Glen_b Jun 09 '16 at 01:53

1 Answers1

21

There is the fitdistr function in the MASS package or some of the functions in the fitdistrplus package. Here are some examples from the latter. 

require(fitdistrplus)

set.seed(1)
dat <- rnorm(50,0,1)
f1 <- fitdist(dat,"norm")
f2 <- fitdist(dat,"logis")
f3 <- fitdist(dat,"cauchy")

so for example 

> f1
Fitting of the distribution ' norm ' by maximum likelihood 
Parameters:
      estimate Std. Error
mean 0.1004483 0.11639515
sd   0.8230380 0.08230325

and you can see the plots with 

plotdist(dat,"norm",para=list(mean=f1$estimate[1],sd=f1$estimate[2]))
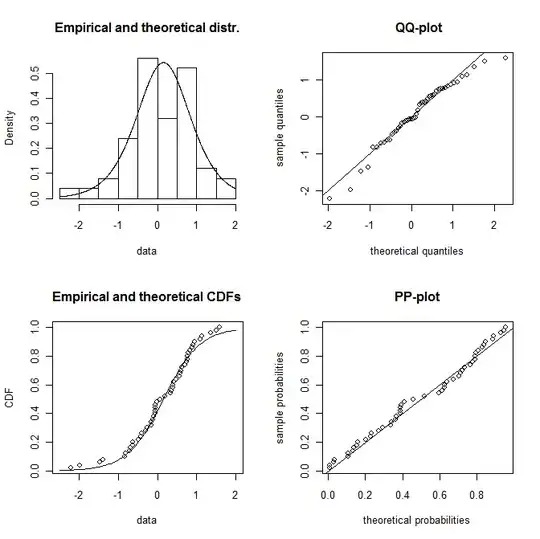
plotdist(dat,"logis",para=list(location=f2$estimate[1],scale=f2$estimate[2]))
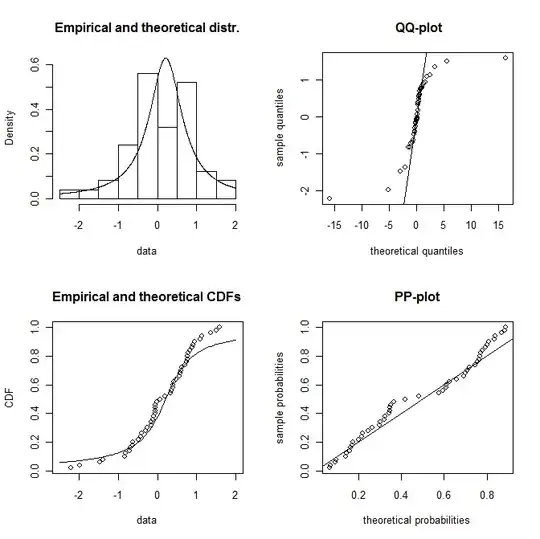
plotdist(dat,"cauchy",para=list(location=f3$estimate[1],scale=f3$estimate[2]))

so it looks plausible as a normal distribution

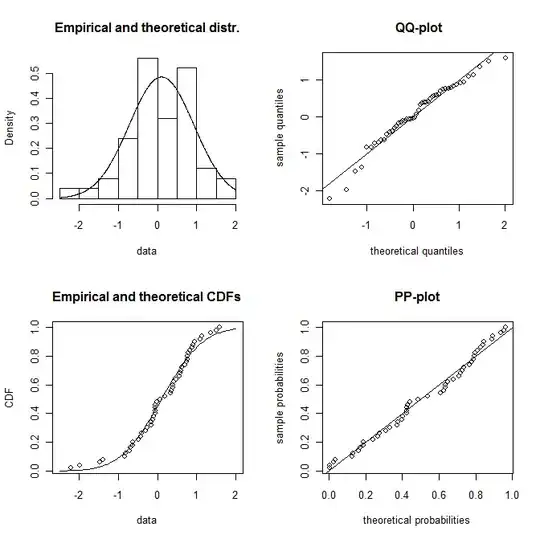
enter image description here

but also perhaps as a logistic distribution (you will need a larger sample to distinguish them in the tails)

enter image description here

though with a qqplot and looking at the CDF you can tell that this is probably not a Cauchy distribution

enter image description here

Henry
  • 30,848
  • 1
  • 63
  • 107
  • 1
    Thank you Henry for a lovely overview. I've been asked if there are any packages that take in data and spit out which distribution (and parameters) spit best. Are you aware of any such functionality in any of the packages? – Roman Luštrik Mar 30 '12 at 22:58
  • 3
    `fitdist` provides estimates of parameters. There are some hints at what the distribution might be from functions such as `descdist(dat, boot = 1000)` but they too would benefit from a larger sample. – Henry Mar 31 '12 at 00:53
  • None of these functions will solve the problem you posed in your last [question](http://stats.stackexchange.com/q/25604/601) when the sample isn't representative. – John Mar 31 '12 at 17:01
  • A comment on the first answer... it looks like f1 – Scott Kaiser Jun 10 '14 at 23:31
  • 1
    @Scott Kaiser: I do not think so. `fitdist()` is a function in the fitdistrplus package, and this is what I was using. Meanwhile `fitdistr()` is a function in the MASS package, and would not work here in this form. – Henry Jun 11 '14 at 06:04
  • 1
    I don't have enough points to add this as a comment, but just as an additional note to the information provided in the thread above, it is also possible to simply call `plot(f1)` instead of the more convoluted `plotdist(dat,"norm",para=list(mean=f1$estimate[1],sd=f1$estimate[2]))` – swestenb Jun 09 '16 at 00:39