PDF for a continuous distribution

Question

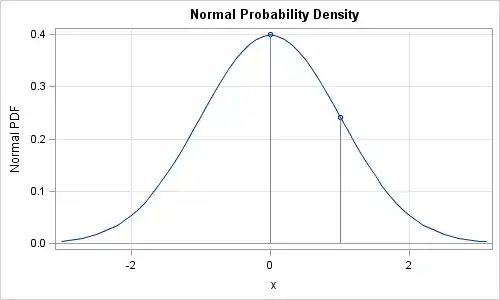
If for a discrete distribution we can say that its PDF answers a question of something like "How possible is exactly this value?", then what would a be similar "human" interpretation of a PDF for a continuous distribution?

And in R, how in some kind of "practical" terms can an illiterate like me interpret something like dnorm(0.2, 0, 1)? What exactly is '0.2'?

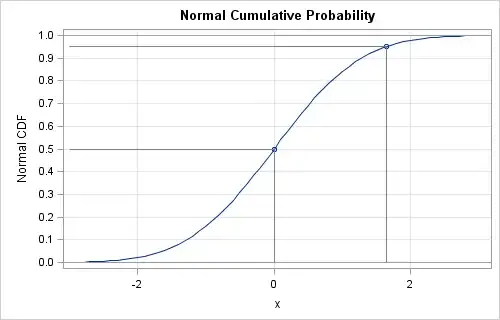
Besides, if dnorm reports a probability for a value in an interval, then is it in any way related to pnorm, which kinda also reports probability for a value in an interval (probability for a value in an upper or in a lower tails)? Can dnorm be expressed via two pnorms? Like, Probability(x1 < X < x2) = F(x2) - F(x1) or something like that?

@Tim, not really. I pretty much understand that an "area under the curve between two distinct points defines the probability for that interval." I.e., the question I'm looking for can be expressed as "How possible is the value in this interval?" But then, how one should interpret `dnorm` input? `dnorm(0.2, 0, 1)`? What exactly is '0.2', how can it be an interval? — katu, Dec 31 '16 at 08:27
@Tim, also, if `dnorm` reports a probability for a value in an interval, then is it in any way related to `pnorm`, which *kinda* also reports probability for a value in an interval (tails)? Can `dnorm` be expressed via two `pnorms`? Like, `Probability(x1 < X < x2) = F(x2) - F(x1)`? — katu, Dec 31 '16 at 08:30
@Tim, there's no mention of `dnorm` on the page you've linked to. — katu, Dec 31 '16 at 08:30
`dnorm` is pdf of normal dissolution and the linked thread is about pdfs. Moreover please read it carefully, pdf is *not* probability that value lies in some given interval. — Tim, Dec 31 '16 at 09:38
One thing that disappoints me in the above mentioned post is that nothing in the answers says the word "limit". which is the key concept here. @katu, if you understand the area under the curve for the probability of the interval, you are almost there. There should be no problem with the probability of the interval, [0.2, 0.2+Δ] where Δ is some number. If Δ is small, the area under the curve is closely approximated by a rectangle with width Δ and some height. As Δ -> 0, the height approaches a constant. So dnorm(0.2) = $lim_Δ->0$ pnorm([0.2,0.2+Δ]). — G5W, Dec 31 '16 at 11:31
@G5W not exactly... as $\Delta\to 0$ `pnorm` will always be <0, while `dnorm` can exceed 1 as noted in the linked thread. It is the opposite, integrating pdf's leads to cdf's. — Tim, Dec 31 '16 at 14:08
@G5W There are good reasons not to introduce limits in these explanations, both pedagogical and technical: the limit approach is not sufficiently general to handle all distributions. As Tim has pointed out, your limit definition is incorrect anyway: you need to divide by $\Delta$. — whuber, Dec 31 '16 at 15:15

gung - Reinstate Monica · Answer 1 · 2017-01-04T16:51:44.067

2

The Cumulative Distribution Function (CDF, sometimes just called the distribution function) of a continuous distribution (like the normal distribution) gives you the proportion of the distribution less than or equal to a given quantile (i.e., a given point in $X$).

The Probability Density Function (PDF) is the derivative of the CDF. That is, it gives the rate of change in the CDF (how fast it is increasing) associated with a given quantile.

It does not give the probability of drawing that quantile from the distribution. It can't, because there is no finite probability associated with a point from a continuous distribution. Remember that in math / geometry, a point has no finite width, and probability is defined as the area under the curve. Thus, we can take the height of the curve at a given quantile $f(x)$ and multiply it by the width, which is infinitely narrow (call it '$0$' if that's easier to think about), and the area will always be infinitely small. This is not intuitive for people, because we think of a point being something like $1.2$, not $1.2\bar{0}$ (where $\bar 0$ means infinitely repeating $0$s); in other words, people think of $1.2$ as the interval $[1.15, 1.25)$, where any value within that interval is $\approx 1.2$. There is a finite probability associated with that, because it does have a finite width (even if small). However, because that has a measurable width, it isn't a point.

edited Jan 04 '17 at 16:51

answered Dec 31 '16 at 14:59

gung - Reinstate Monica

132,789
81
357
650

1

+1 but regarding `there is no finite probability associated with a point from a continuous distribution` - zero is finite. – amoeba Jan 04 '17 at 13:28
1

@amoeba, I would say that if the probability associated w/ every point in the distribution's support is $0$, then the probability of any point must be $0$--the distribution integrates to $0$ rather than $1$. The way I would put it is that the probability is infinitely small / infinitely close to $0$, but not quite. This gets to be a pretty rarefied discussion, though. – gung - Reinstate Monica Jan 04 '17 at 13:48
I don't think I follow. As I am sure you know, the probability of any given point is exactly zero ("infinitely close to zero but not quite" is not a well-defined mathematical term, unless you are thinking [nonstandard analysis](https://en.wikipedia.org/wiki/Non-standard_analysis)); didn't you write in this very answer that "the area will always be zero"? The integral is of course non-zero; that's how measure works: points have measure zero, but intervals, even though they are composed of points, have non-zero measure. – amoeba Jan 04 '17 at 14:31
In any case, I was simply noticing that you wrote in this answer that the area "will always be zero" but also that there is "no finite probability". This sounds as a contradiction to me because zero is finite. – amoeba Jan 04 '17 at 14:34
@amoeba, you're right, that was inconsistent. I have tried to make it more consistent. Let me know if it isn't clear. What I meant was that the width of a point is an [infinitesimal](https://en.wikipedia.org/wiki/Infinitesimal), & thus so is the probability. – gung - Reinstate Monica Jan 04 '17 at 16:53
It's more consistent now, but I am still confused about why you don't want to say that probability of any point is zero. Do you just want to avoid saying that, for some pedagogical reasons? Or do you actually think it's not true? I mean, it is a standard fact, see http://stats.stackexchange.com/questions/60702 or http://math.stackexchange.com/questions/180283 or pretty much everywhere else. "Infinitesimal" is not really a formal term in standard mathematics. If e.g. $X\sim\mathcal N(0,1)$ then $P(X=0)$ is a well-defined mathematical quantity. Its value exists and it is zero. Do you disagree? – amoeba Jan 04 '17 at 17:06
@amoeba, I don't think of the idea of an infinitesimal as being so exotic (but then, I'm an old man). If we are committed to the idea that the probability associated w/ every possible point is *literally* $0$, then integrating over an infinite number of $0$s must equal $0$. At the end of the intro to the Wikipedia page it says, "Vladimir Arnold wrote in 1990: Nowadays, when teaching analysis, it is not very popular to talk about infinitesimal quantities. Consequently present-day students are not fully in command of this language. Nevertheless, it is still necessary to have command of it". – gung - Reinstate Monica Jan 04 '17 at 17:32
Arnold loved provocative statements; without context I am not sure what exactly he meant in this case. Infinitesimals have meaning in [Robinson](https://en.wikipedia.org/wiki/Abraham_Robinson)'s so called [nonstandard analysis](https://en.wikipedia.org/wiki/Non-standard_analysis) which *is* exotic, and very much so. In standard math there are no infinitesimals, and measure of a point is "literally" zero but an integral over an interval is not. The conditional statement in your second sentence is simply false. Unless you are following Robinson and rejecting most of the standard math. – amoeba Jan 04 '17 at 17:42
See e.g. https://en.wikipedia.org/wiki/Lebesgue_measure#Examples, bullet four. – amoeba Jan 04 '17 at 17:45
1

You seem to be right, @amoeba. Curious... I remember talking about infinitesimals when I took calculus (or at least, I think I remember that--I could swear that was what Gottfried kept saying). – gung - Reinstate Monica Jan 04 '17 at 18:58
Haha, I like your last comment, @Gungsun. There is a lot about epsilon-delta notation in basic calculus classes, and it's easy to be sloppy about it and think about epsilon as an "infinitesimal number". This is similar to thinking about delta function as a "function that is zero everywhere and infinitely high at zero, integrating to one" even though such function obviously does not exist, so delta function, when done properly, is actually defined quite differently... But Leibniz when introducing calculus, similarly to Dirac when introducing delta function, were often sloppy. It worked though. – amoeba Jan 04 '17 at 20:29

PDF for a continuous distribution

1 Answers1