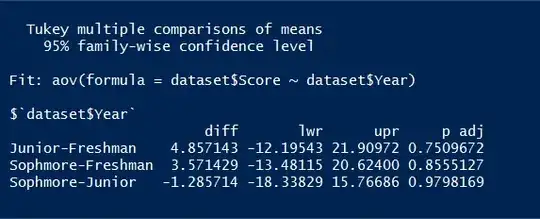
I performed a simple ANOVA in R and then generated the following TukeyHSD() comparisons of means:
I have a pretty good idea (I think) of what all this means except the 'p adj'. If I'm correct:
- The difference in test scores between say Juniors and Freshmen is 4.86, with Juniors averaging 4.86 points higher.
- The 95% confidence interval of that difference is between -12.19 and 21.91 points.
But it's not clear to me what the p adj represents. First of all, adjusted for what? Secondly, is this to be interpreted like any other p-value? So, between juniors and freshmen there is no statistical difference in the means (because the p-value > .05)?