I would have to define, in R, a mixture of a number of bivariate normal distributions like that: 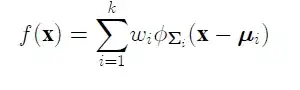
a strategy would be to define the single pieces of the expressions, for example:
bivn_1 <- mvrnorm(1000, mu = c(0, 0), Sigma = matrix(c(1, 0, 0, 1), 2))
bivn_2 <- mvrnorm(1000, mu = c(.5, .5), Sigma = matrix(c(.4, 0, 0, .4), 2))
....
and then to sum up the pieces with the weights $w_1, w_2.... w_n$
Is there a different and easier strategy?