Are there any non-identical distributions which happen to have the same moment-generating function?
-
4See Wikipedia under [Moment-generating function#Important properties](http://en.wikipedia.org/wiki/Moment-generating_function#Important_properties) – onestop Mar 21 '12 at 15:17
-
@onestop that answers it! if you want to put that as an answer I'll accep tit. – Mar 21 '12 at 15:52
1 Answers
Yes.
In an exercise, Stuart & Ord (Kendall's Advanced Theory of Statistics, 5th Ed., Ex. 3.12) quote a 1918 result of TJ Stieltjes (which apparently appears in his Oeuvres Completes,):
If $f$ is an odd function of period $\frac{1}{2}$, show that
$$\int_0^\infty x^r x^{-\log x} f(\log x) dx = 0$$
for all integral values of $r$. Hence show that the distributions
$$dF = x^{-\log x}(1 - \lambda \sin(4\pi \log x))\ dx, \quad 0 \le x \lt \infty;\quad 0 \le |\lambda| \le 1,$$
have the same moments whatever the value of $\lambda$.
(In the original, $|\lambda|$ appears only as $\lambda$; the restriction on the size of $\lambda$ arises from the requirement to keep all values of the density function $dF$ non-negative.) The exercise is easy to solve via the substitution $x = \exp(y)$ and completing the square. The case $\lambda=0$ is the well-known lognormal distribution.
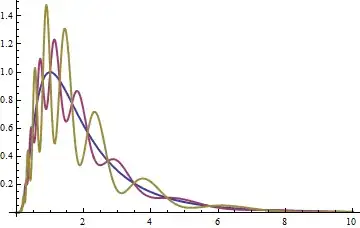
The blue curve corresponds to $\lambda=0$, a lognormal distribution. For the red curve, $\lambda = -1/4$ and for the gold curve, $\lambda = 1/2$.
- 281,159
- 54
- 637
- 1,101
-
8But the [lognormal distribution](http://en.wikipedia.org/wiki/Lognormal_distribution) does not have a moment-generating function. – onestop Mar 21 '12 at 16:44
-
6That's an excellent point, onestop, and I have to agree with it. I took the question in the sense of "having the same set of moments" and I should have pointed out that change of interpretation. When the mgf exists *as a function* (and not just as a formal power series) then it can be inverted to produce a unique density to which it corresponds. – whuber Mar 21 '12 at 16:55
-
Its not true that the lognormal dont have mgf, its only that its not defined on an *open* interval containing zero – kjetil b halvorsen Apr 21 '17 at 07:10
-
..... see http://link.springer.com/article/10.1007/s11009-014-9430-7 – kjetil b halvorsen Apr 21 '17 at 08:44
-
2For the record, both @onestop and I were implicitly discussing the existence of an mgf *in a neighborhood of $0.$* This sense is often assumed because one of the most basic uses of an mgf is to expand its MacLaurin series (Taylor series around $0$) to compute or analyze the moments and this requires the function to be defined in a neighborhood, not just at $0.$ – whuber Feb 01 '19 at 20:27
-
1@whuber: That's OK, but it seems to be understood implicitely so often that one forgets that mgf's can be useful otherwise too. See also (the links in) https://stats.stackexchange.com/questions/389846/moment-generating-function-for-lognormal-random-variable/390185#390185 – kjetil b halvorsen Feb 02 '19 at 17:59
-
Should *for all integral values of $r$* be *for all integer values of $r$*? If not, what does *integral* mean in this context? – Richard Hardy Mar 05 '21 at 06:38
-
@Richard "integer values" is poor grammar; "integral values" means "values that are integers." – whuber Mar 05 '21 at 14:37
-
@whuber, thank you. This was beyond my knowledge of English (not a native speaker). – Richard Hardy Mar 05 '21 at 14:45