24

Given a hierarchical model $p(x|\phi,\theta)$, I want a two stage process to fit the model. First, fix a handful of hyperparameters $\theta$, and then do Bayesian inference on the rest of the parameters $\phi$. For fixing the hyperparameters I am considering two options.

  1. Use Empirical Bayes (EB) and maximize the marginal likelihood $p(\mbox{all data}|\theta)$ (integrating out the rest of the model which contains high dimensional parameters).
  2. Use Cross Validation (CV) techniques such as $k$-fold cross validation to choose $\theta$ that maximizes the likelihood $p(\mbox{test data}|\mbox{training data}, \theta)$.

The advantage of EB is that I can use all data at once, while for CV I need to (potentially) compute the model likelihood multiple times and search for $\theta$. The performance of EB and CV are comparable in many cases (*), and often EB is faster to estimate.

Question: Is there a theoretical foundation that links the two (say, EB and CV are the same in the limit of large data)? Or links EB to some generalizability criterion such as empirical risk? Can someone point to a good reference material?

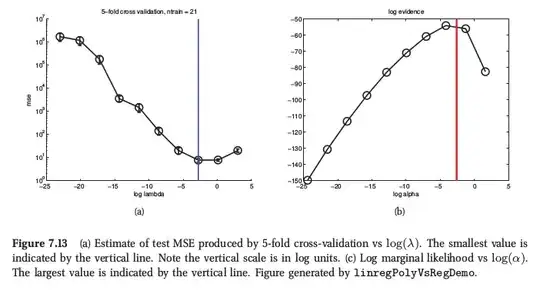
(*) As an illustration, here is a figure from Murphy's Machine Learning, Section 7.6.4, where he says that for ridge regression both procedures yield very similar result:

murphy - empirical bayes vs CV

Murphy also says that the principle practical advantage of the empirical Bayes (he calls it "evidence procedure") over CV is when $\theta$ consists of many hyper-parameters (e.g. separate penalty for each feature, like in automatic relevancy determination or ARD). There it is not possible to use CV at all.

amoeba
  • 93,463
  • 28
  • 275
  • 317
Memming
  • 1,570
  • 12
  • 23
  • Can you describe in more detail what you're doing for the cross-validation method? Are you fixing $\theta$ and then using the training data to estimate the other parameters before validating? – Neil G Mar 17 '12 at 22:55
  • @NeilG maximizing the sum of log marginal predictive data likelihood on cross-validation sets (k is integrated out). – Memming Mar 17 '12 at 23:32
  • 1
    If $k$ is integrated out both times, then what's the difference between CV and EB? – Neil G Mar 18 '12 at 00:30
  • 2
    Great question. I took the liberty to add a figure from Murphy's textbook to your question to illustrate your point about two procedures often being comparable. I hope you will not mind this addition. – amoeba Jan 27 '17 at 10:48

2 Answers2

18

I doubt there will be a theoretical link that says that CV and evidence maximisation are asymptotically equivalent as the evidence tells us the probability of the data given the assumptions of the model. Thus if the model is mis-specified, then the evidence may be unreliable. Cross-validation on the other hand gives an estimate of the probability of the data, whether the modelling assumptions are correct or not. This means that the evidence may be a better guide if the modelling assumptions are correct using less data, but cross-validation will be robust against model mis-specification. CV is assymptotically unbiased, but I would assume that the evidence isn't unless the model assumptions happen to be exactly correct.

This is essentially my intuition/experience; I would also be interested to hear about research on this.

Note that for many models (e.g. ridge regression, Gaussian processes, kernel ridge regression/LS-SVM etc) leave-one-out cross-validation can be performed at least as efficiently as estimating the evidence, so there isn't necessarily a computational advantage there.

Addendum: Both the marginal likelihood and cross-validation performance estimates are evaluated over a finite sample of data, and hence there is always a possibility of over-fitting if a model is tuned by optimising either criterion. For small samples, the difference in the variance of the two criteria may decide which works best. See my paper

Gavin C. Cawley, Nicola L. C. Talbot, "On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation", Journal of Machine Learning Research, 11(Jul):2079−2107, 2010. (pdf)

Dikran Marsupial
  • 46,962
  • 5
  • 121
  • 178
  • Why do you say that CV is robust against a mis-specified model? In his case, there is no such protection since cross-validation is searching over the same space that EB is calculating a likelihood. If his modelling assumptions are wrong, then cross-validation won't save him. – Neil G Mar 18 '12 at 00:40
  • 2
    CV is robust against misspecification in the sense that it still gives a useful indicator of generalisation performance. The marginal likelihood may not as it depends on the prior on $\phi$ (for example), even after you have marginalised over $\phi$. So if your prior on $\theta$ was misleading, the marginal likelihood may be a misleading guide to generalisation performance. See Grace Wahba's monograph on "spline models for observational data", section 4.8 (it doesn't say a great deal, but there isn't much on this topic AFAIK). – Dikran Marsupial Mar 19 '12 at 09:44
  • p.s. I have been performing an analysis of avoiding overfitting in neural networks with Bayesian regularisation where the regularisation parameters are tuned via marginal likelihood maximisation. There are situations where this works very badly (worse than not having any regularisation at all). This seems to be a problem of model mis-specification. – Dikran Marsupial Mar 19 '12 at 09:45
  • He can get the same "indicator of generalization performance" by checking the total log-probability of the data given the estimated distribution returned by EB (which will be equal to the entropy of that distribution). There's no way to beat it in this case because it is the analytical solution to this problem. I don't see why cross-validation would makes sense when you can calculate a likelihood for EB. – Neil G Mar 19 '12 at 09:50
  • Spline models and neural network are good examples where you can't calculate a likelihood over all of the parameters (for example, degree of the spline, neural network size and number of connections) and so those are examples where cross-validation gives you the ability to make good choices for those parameters. Maybe there's a hole in my understanding because I don't see what exactly is different about those parameters. What do you think? – Neil G Mar 19 '12 at 09:52
  • Regarding robustness of cv - I though cv was still sensitive to the choice of measure for the loss function. This is mathematically the same thing as the evidence being sensitive to choice of likelihood function, isnt it? it seems more like "conceptual robustness" rather than anything real. – probabilityislogic Mar 19 '12 at 10:19
  • @Neil G, there is a closed form expression for the cross-validation error of many models as well (e.g. Gaussian Processes). As I said, it isn't the same indicator of generalisation performance, as it depends on the stochastic model (as Wahba puts it). You gan have two Bayesian models that give the same predictions everywhere, but which have very different marginal likelihoods, but they would have assympotically similar cross-valdiation estimates. – Dikran Marsupial Mar 19 '12 at 11:06
  • Choosing the hidden layer size is a clear example of the $\theta$ in the original question, where the weights the $\phi$ have been marginalised. In that case, choosing the hidden layer size by maximising the marginal likelihood works very badly on some datasets. – Dikran Marsupial Mar 19 '12 at 11:09
  • 2
    @probabilityislogic, I'm not quite sure what you are getting at (problem undoubtely at my end! ;o). I can tell you from practical experience though that the issue is very real. I have been working on problems in model selection for several years, and I have come across many problems where maximising the marginal likelihood turns out to be a very bad idea. Cross-validation performs about as well for most datasets, but where it performs badly it rarely performs catastrophically as evidence maximisation sometimes does. – Dikran Marsupial Mar 19 '12 at 11:12
  • @probabilityislogic - note the model assumptions includes the prior as well as the likelihood. I'm not saying CV is necessarily better than marginal likelihood. For example for a GP, if the covariance function were inappropriate, marginal likelihood maximisation will choose the hyper-parameters assuming that the covariance function is right, but we have an odd sample of data from that prior, but cross-validation will choose hyper-parameters that compensate somewhat for this in order to maximise performance on the validation folds. – Dikran Marsupial Sep 07 '12 at 17:30
-1

If you didn't have the other parameters $k$, then EB is identical to CV except that you don't have to search. You say that you are integrating out $k$ in both CV and EB. In that case, they are identical.

Neil G
  • 13,633
  • 3
  • 41
  • 84