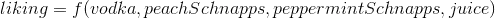5

What are the difference between a linear mixed model with random slope and intercept and a linear model with an interaction effect?

If I predict the effect of 1) the main effect and 2) the random effect / the interaction, I get different results and am wondering about the reasons.

Take the following example: 

# simulate data
set.seed(999)
response <-  rnorm(200, 100, 50)

set.seed(777)
dev <- rnorm(response, 0, 50)

DF <- data.frame(response = response) %>% 
  mutate(pred = response + dev) %>% 
  arrange(response) %>% 
  mutate(factor = rep(LETTERS[1:4], each = 50)) 

# classical linear model
mod.lm <- lm(response ~ pred * factor, data = DF)

PRED <- predict(mod.lm, type = "terms")
Const <- attr(PRED,"constant")

# predict
PRED.df <-  data.frame(y = PRED) %>% 
  mutate(y.pred = y.pred + Const) %>% 
  mutate(y.factor = y.factor + Const) %>% 
  mutate(y.pred.factor = y.pred + y.factor + y.pred.factor - Const) %>% 
  mutate(x = as.vector(DF$pred)) %>% 
  mutate(factor = as.vector(DF$factor))

#plot
ggplot(DF,aes(x = pred, y = response, colour = factor))+
  geom_point()+
  geom_line(data = PRED.df, aes(x = x, y = y.pred), colour = "black")+
  geom_line(data = PRED.df, aes(x = x, y = y.pred.factor))+
  labs( title = "lm(response ~ pred * factor, data = DF)")


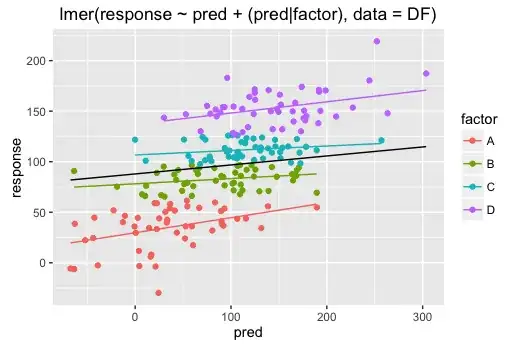
# linear mixed model with lme4
mod.lme4 <- lmer(response ~ pred + (pred|factor), data = DF)

# predict
PRED.lme4 <- 
  data.frame(y = predict(mod.lme4, re.form = NA)) %>% 
  mutate(y2 = predict(mod.lme4, re.form = ~ (pred|factor))) %>% 
  mutate(x = as.vector(DF$pred)) %>% 
  mutate(factor = as.vector(DF$factor))

# plot
ggplot(DF,aes(x = pred, y = response, colour = factor))+
  geom_point()+
  geom_line(data = PRED.lme4, aes(x = x, y = y), colour = "black")+
  geom_line(data = PRED.lme4, aes(x = x, y = y2))+
  labs( title = "lmer(response ~ pred + (pred|factor), data = DF)")

gives

linear model

and

linear mixed model

I agree that the differences are not huge but still appreciable (and will also depend on the data)

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
Latrunculia
  • 201
  • 1
  • 7
  • 1
    It's not *technically* Bayesian (rather, "frequentist shrinkage estimator"), but yes. Voting to move to CrossValidated – Ben Bolker Nov 24 '16 at 22:02
  • 1
    You need to consider the context in which you would have a varying slope. For example, repeated measure design where each subject does both control and experimental condition. Here, you must consider variation in subject and treatment. The data you generated does not have a multilevel structure. You should make data where the factor and pred account for variation in the outcome. An improperly specified model in this situation, for example using lm, can greatly inflate the type one error rate as the standard error is often underestimated. – D_Williams Nov 25 '16 at 04:55
  • Check http://stats.stackexchange.com/questions/120964/fixed-effect-vs-random-effect-when-all-possibilities-are-included-in-a-mixed-eff/137837#137837 – Tim Nov 25 '16 at 08:13

0 Answers0