How to prevent newton's method from finding maxima?

Question

Let's say I'm trying to find a minimum of a function f(x). I know I can find a local extrema of f(x) by using newton's method to solve f'(x) = 0. Is there a way to modify Newton's method so that I'm sure I find a local minimum and not a local maximum?

Answer 1

To find all local minima, we 1) find all minima, $x_1$, such that $f'(x_1)=0$, and 2) for a constrained solution test for local minima at the extreme $x$-values.

If $f''(x_1)>0$ then $f(x_1)$ is a local (or global) minimum. That is, slope changes (curves) positively in the region of a local minimum.

If $f''(x_1)<0$ then $f(x_1)$ is a local maximum. That is, slope changes negatively in the region of a local maximum.

Example, for $f(x)=\sin(x)$ then $f'(x)=\cos (x)$ and $f''(x)=-\sin (x)$ Then for $0\leq x\leq 2 \pi$, $f'(x)=\cos (x)=0\to x_1=\frac{\pi }{2},x_2=\frac{3 \pi }{2}$

Since $f''(x_1)=-\sin (\frac{\pi }{2})=-1<0$, $f(\frac{\pi }{2})$ is a local (or global) maximum. Moreover, for $f''(x_2)=-\sin (\frac{3\pi }{2})=1>0$, $f(\frac{3\pi }{2})$ is a local (or global) minimum.

These situations are shown in the plot below.

The OP's question is how to avoid finding maxima at all. Probably the easiest to understand way to do that is to grid search for $f''(x_1)>0$ regions and to start Newton's method in the center of each such region. One could also try to modify Newton's method so that it only searches in a region when a trial left-hand slope is less than a trial right hand slope, (note the left hand slope of two point slopes can be sequentially the first or the second one calculated, so this gets a bit confusing). However, it then becomes difficult to know when to stop the algorithm, that is, if one want to recover all of the local minima.

Problems. Newton's method applies to finding the solutions of functions with smooth derivatives. In this case, Newton's method is being applied to the first derivative of a function as opposed to finding $f(x)=0$. Thus, we are assuming that the first derivative is smooth and as Newton's method relies on the smoothness of the derivative of the search function, we are also given that the second derivative is smooth as well. This implies that certain functions cannot be solved, for example, the pathological Weierstrass function that is continuous everywhere but so unsmooth that it is nowhere differentiable.

Constrained versus unconstrained solutions. If we apply Newton's method to the unconstrained (i.e., full) range of a function with infinite or semi-infinite support, it is easy to understand that for functions with a tail or tails that are asymptotic to zero, but do not reach zero, that the method will not converge when initiated in the tail region. The alternative is to constrain the regions of search.

Thus, doing a (constrained) grid search to apply Newton's method is appealing. If we do not start our search close to the root we are trying to find we may miss finding that root entirely, see this, for example. Also, in initiating our grid search for finding $f(x)$ minima (i.e., those $f'(x)$ roots with $f''(x)>0$), we have to test the endpoints of our constrained search in a different manner than using $f'(x)=0$ with $f''(x)>0$ for the interior points. This is because a local minimum can be formed by the discontinuities at those endpoints, which is different from the support for interior points. At the left hand endpoint, $\min(x)$, it is sufficient that $f'[\min(x)]>0$ for that endpoint to be a local minimum of $f(x)$. In like manner, for the right hand endpoint, $\max(x)$, it is sufficient that $f'[\max(x)]<0$ for $\max(x)$ to be the location of a local minimum of $f(x)$.

In our example plot above, testing of the endpoints for $0\leq x\leq 2 \pi$ would give us a local minimum at $f(0)=0$, and from $f'(\frac{3\pi }{2})=0$, where $f''(\frac{3\pi }{2})>0$, then $f(\frac{3\pi }{2})$ is a local (or global) minimum. Finally, since $f(\frac{3\pi }{2})=-1 < f(0)=0$, then $f(\frac{3\pi }{2})$ is the global minimum for $0\leq x\leq 2 \pi$.

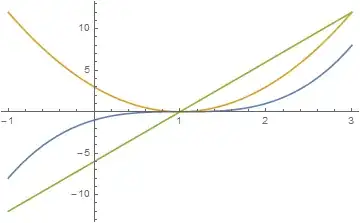
Finally, note that we did not classify $f'(0)=0$ and $f''(x)=0$, which may be indeterminate (e.g., for a flat line it is both a global minimum and maximum) but which can be neither a minimum or a maximum, e.g., at a zero-slope, inflection and saddle point. For example, let $f(x)=x^3-3 x^2+3 x-1$, then $f(1)=0,f'(1)=0,f''(1)=0$ and the plot of $f(x)$ and its first two derivatives in blue orange and green, respectively, is

Answer 2

Yes, you can also combine the Newton's with the Gradient Decent, by adding a regularized part:

$$(\mathbf H + r\mathbf I) dx = \nabla f$$

Setting the regularizer $r$ to a proper value, will give you a stable direction to the minima. And when $r = 0$, it becomes the original Newton's method.