If the function $f(x)$ is continuous and a probability density function (PDF), how can I show that its mode is at $f'(x)=0$?
-
3As per Christoph's answer, this does not hold. Not even if $f$ is everywhere differentiable (it could have a vanishing derivative at a minimum at the extremes of its domain of definition). – Stephan Kolassa Oct 08 '15 at 11:53
-
1@Stephan The logic of the question is a little different. It does not ask to show that all points of vanishing derivative are modes, but only that the derivative at a mode must vanish. (The only way that can fail to be true is when $f$ is not differentiable at its mode.) – whuber Oct 08 '15 at 15:01
-
1you might read it either way, I guess: show that its mode is at $f'(x)=0$ seems compatible with the aim to show the (false, as we discussed) implication $f'(x)=0\Rightarrow\text{a mode}$ – Christoph Hanck Oct 08 '15 at 16:08
2 Answers
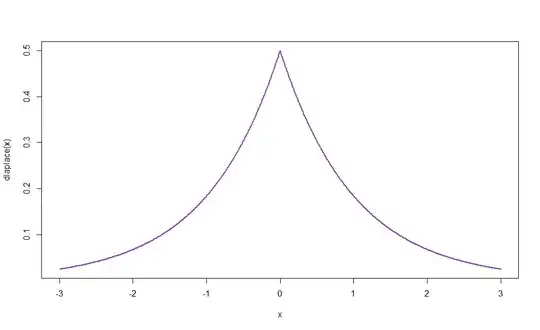
If it's only continuous but not differentiable at the mode, you can't. Consider the Laplace distribution.
- 25,948
- 3
- 57
- 106
-
Also see https://en.wikipedia.org/wiki/Uniform_distribution_(continuous)#/media/File:Uniform_Distribution_PDF_SVG.svg, the density for the continuous uniform distribution on [a, b]. There are points outside [a, b] where df/dx = 0. – Adrian Oct 08 '15 at 12:23
-
Same comment as above, but better example: https://en.wikipedia.org/wiki/Triangular_distribution#/media/File:Triangular_distribution_PMF.png, the triangular distribution (can be generated as the sum of two iid uniforms). – Adrian Oct 08 '15 at 12:40
-
Better than my first comment, but not better than your answer! My comments were intended as additional examples for the OP, not as contradicting your answer. – Adrian Oct 08 '15 at 13:16
-
1@Adrian The uniform distribution is not a valid counterexample, because no version of its density can be continuous, as required by the question. – whuber Oct 08 '15 at 14:59
Find the maximum value. The Laplace distribution is defined piece-wise, and not smooth at the mode, which is at the piece-wise common point (A.K.A., corner point), and such a common, junctional corner point in a piece-wise defined function has no general continuity guarantee of either the separate piecewise defined functions' amplitudes nor any of their derivatives. The mode for a Laplace distribution occurs at $\frac{e^{-\frac{x-\mu }{\beta }}}{2 \beta }=\frac{e^{-\frac{\mu -x}{\beta }}}{2 \beta }\to x=\mu$, because $f(x=\mu)=\frac{1}{2 \beta }$ is the maximum value of $f$. Of course there are continuous functions that are differentiable nowhere, and differentiability is not a requirement. Thus, the general answer is simply find the maximum of the pdf. This can be done in closed form as above for something as simple as the Laplace distribution. It can be done numerically for nice smooth functions using derivatives example by referring to How to prevent newton's method from finding maxima? and altering it to avoid minima. Or, more generally for nasty functions using a canned routine like FindMaximum in Mathematica with a global search routine like RandomSearch.
@Glen_b and @Dougal, thanks for the help, anything further @me.
-
2The mode is *not* at a boundary for the Laplace (which is defined - and continuous - over the whole real line). It's *not* cheating but a perfectly valid counterexample. If people don't account for such possibilities, they will be wrong when they try to make general statements. I suspect you misunderstand what a boundary is in this case (an example of a case where you'd worry about the mode being at a boundary would be the case of an ordinary exponential distribution at 0). – Glen_b Mar 26 '17 at 09:01
-
2@Carl If you define the Laplace distribution piecewise for the negative and positive reals, then sure, the mode 0 is at a boundary of each sub-part. But in the standard way of thinking about it, the Laplace density is just a function $\frac12 \exp(- \lvert x \rvert )$ defined on $\mathbb R$, and $0$ is in no way a boundary point of $\mathbb R$. – Danica Mar 26 '17 at 16:45
-
@Carl In this case we're talking about a boundary point of the domain of the variable. The random variable is defined over the whole real line, so for the Laplace, the set $A$ in the definition you quote is $\mathbb{R}$. – Glen_b Mar 26 '17 at 17:11
-
Carl: You can't just define a point in the middle to be a part of the boundary. The actual domain is the union of your two subsets, and there's no boundary point between them. Otherwise what would stop me saying *exactly what you said* but about (say) the normal density? (... and yes, this is indeed *semantics* -- it's precisely about what the term "boundary" actually means) – Glen_b Mar 27 '17 at 05:22
-
2There's only a junction there because you chose to make it one; that's not necessary to anything. It doesn't matter *how* you want to split a domain up, that doesn't make it a boundary. The domain *is* the union of the two pieces you split it into and if you look back at the definition of boundary you gave, and apply it, you can *see* there's no boundary point there. I don't propose to keep arguing with you, though. Your answer is wrong, I've explained why, and you refuse to change it. That's up to you. End of discussion. If you want to argue with the people over on math.SE that's up to you. – Glen_b Mar 27 '17 at 05:48
-
The point at $\mu$ is called a corner point of the function (there are other possible names depending on what aspect of it you want to emphasize, for example it's a point of discontinuity of the derivative, ...), but any such name is irrelevant to whether it's a boundary point -- it simply doesn't meet the definition. [It's also 20 hours since I first commented ... and we've had a number of comments back and forth since; you can hardly claim I've been hasty. Please @me to let me know if you change the answer] – Glen_b Mar 27 '17 at 06:01
-
@Glen_b Took awhile, finally got your POV. My thinking was "not" standard, and [not even wrong](https://en.wikipedia.org/wiki/Not_even_wrong). – Carl Mar 27 '17 at 06:50
-
1I removed my downvote. I still don't agree that the corner in the Laplace is in any sense cheating. It's simply a counterexample to the uncritical use of the derivative -- continuous functions can have corners. – Glen_b Mar 27 '17 at 07:13
-
@Glen_b Fine, removed that too. Now I just say that it is not smooth at the mode. – Carl Mar 27 '17 at 07:54