Laplace smoothing understanding implementation

Question

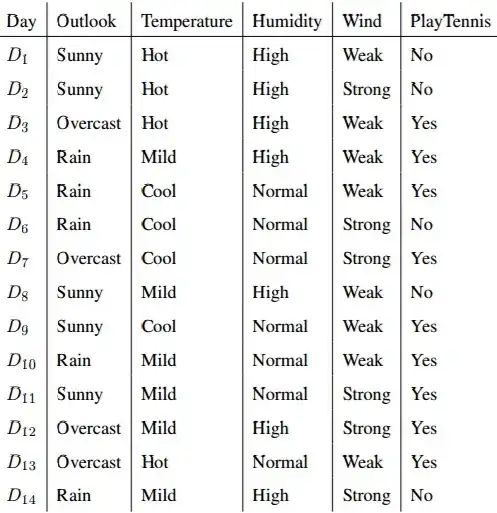
Considering the data set given below

Here if we have to classify new data point:

D15 (O=Overcast, T=Cool, H=High, W=Strong)

Then for P(No|Overcast, Cool, High, Strong)

we have, (5/14) * 0 * (1/5) * (4/5) * (3/5)

This results to 0

So I read that this situation needs smoothing. But what I couldn't figure out is why do we need to smooth this data and how to smooth this data.

Also, does smoothing give better predictions?

Could you please explain me how Laplace smoothing works on this case? I can find some articles in google but non of them were explained in plain simple manner, such that it would help a beginner like me understand it easily.

Answer 1

Actually the above answer is a little incorrect in that, when we are adding 1 to a zero element, we should also divide by P(Y)+1 so that would be:

$\frac{5}{14} \cdot \frac{0+1}{5+1} \cdot \frac{1+1}{5+1} \cdot \frac{4+1}{5+1} \cdot \frac{3+1}{5+1} = 0.011$

Answer 2

The data samples suggest tennis would never be played on overcast days irrespective of the temperature, humidity and wind. Is this realistic or do we lack a sufficient number of samples? Specifically note that tennis is being played on rainy days (i.e. with clouds in the sky like on overcast days), also if it's cool, humidity is high and the wind is strong.

As it seems a bit "harsh" to set the probability of tennis being played on overcast days to 0, smoothing may help. Applying "add-one smoothing":

$\frac{5}{14} * \frac{0+1}{0+1} * \frac{1+1}{5+1} * \frac{4+1}{5+1} * \frac{3+1}{5+1} = 0.066$