My answer premises that the OP does not already know what observations are outliers because if the OP did then data adjustments would be obvious. Thus part of my answer deals with identification of the outlier(s)
When you construct an OLS model ($y$ versus $x$), you get a regression coefficient and subsequently the correlation coefficient I think it may be inherently dangerous not to challenge the "givens" . In this way you understand that the regression coefficient and its sibling are premised on no outliers/unusual values. Now if you identify an outlier and add an appropriate 0/1 predictor to your regression model the resultant regression coefficient for the $x$ is now robustified to the outlier/anomaly. This regression coefficient for the $x$ is then "truer" than the original regression coefficient as it is uncontaminated by the identified outlier. Note that no observations get permanently "thrown away"; it's just that an adjustment for the $y$ value is implicit for the point of the anomaly. This new coefficient for the $x$ can then be converted to a robust $r$.
An alternative view of this is just to take the adjusted $y$ value and replace the original $y$ value with this "smoothed value" and then run a simple correlation.
This process would have to be done repetitively until no outlier is found.
I hope this clarification helps the down-voters to understand the suggested procedure . Thanks to whuber for pushing me for clarification. If anyone still needs help with this one can always simulate a $y, x$ data set and inject an outlier at any particular x and follow the suggested steps to obtain a better estimate of $r$.
I welcome any comments on this as if it is "incorrect" I would sincerely like to know why hopefully supported by a numerical counter-example.
EDITED TO PRESENT A SIMPLE EXAMPLE :
A small example will suffice to illustrate the proposed/transparent method of “obtaining of a version of r that is less sensitive to outliers” which is the direct question of the OP. This is an easy to follow script using standard ols and some simple arithmetic . Recall that B the ols regression coefficient is equal to r*[sigmay/sigmax).
Consider the following 10 pairs of observations.
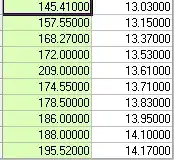
And graphically
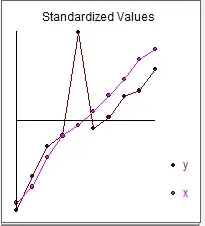
The simple correlation coefficient is .75 with sigmay = 18.41 and sigmax=.38
Now we compute a regression between y and x and obtain the following
Where 36.538 = .75*[18.41/.38] = r*[sigmay/sigmax]
The actual/fit table suggests an initial estimate of an outlier at observation 5 with value of 32.799 . 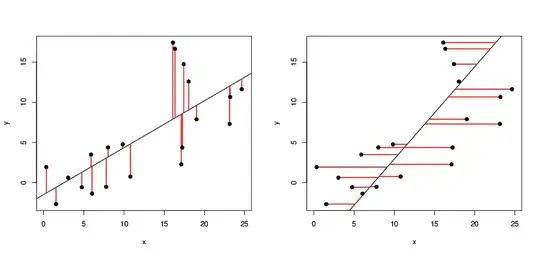
If we exclude the 5th point we obtain the following regression result

Which yields a prediction of 173.31 using the x value 13.61 . This prediction then suggests a refined estimate of the outlier to be as follows ; 209-173.31 = 35.69 .
If we now restore the original 10 values but replace the value of y at period 5 (209) by the estimated/cleansed value 173.31 we obtain 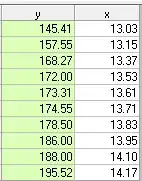
and 
Recomputed r we get the value .98 from the regression equation
r= B*[sigmax/sigmay]
.98 = [37.4792]*[ .38/14.71]
Thus we now have a version or r (r =.98) that is less sensitive to an identified outlier at observation 5 . N.B. that the sigmay used above (14.71) is based on the adjusted y at period 5 and not the original contaminated sigmay (18.41). The effect of the outlier is large due to it's estimated size and the sample size. What we had was 9 pairs of readings (1-4;6-10) that were highly correlated but the standard r was obfuscated/distorted by the outlier at obervation 5.
There is a less transparent but nore powerfiul approach to resolving this and that is to use the TSAY procedure http://docplayer.net/12080848-Outliers-level-shifts-and-variance-changes-in-time-series.html to search for and resolve any and all outliers in one pass. For example 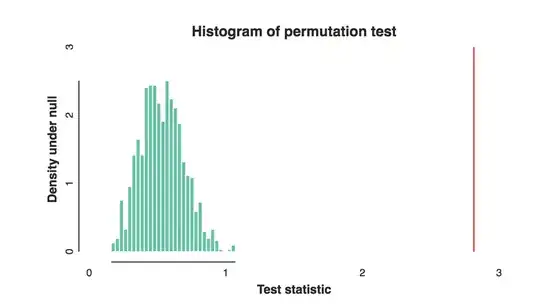 suggsts that the outlier value is 36.4481 thus the adjusted value (one-sided) is 172.5419 . Similar output would generate an actual/cleansed graph or table.
suggsts that the outlier value is 36.4481 thus the adjusted value (one-sided) is 172.5419 . Similar output would generate an actual/cleansed graph or table. 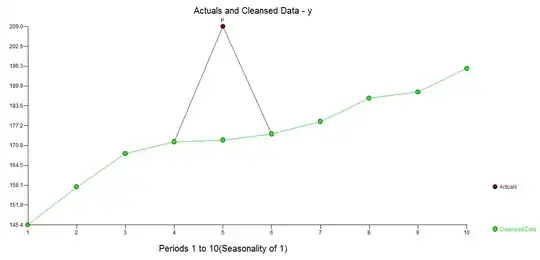 . Tsay's procedure actually iterativel checks each and every point for " statistical importance" and then selects the best point requiring adjustment. Time series solutions are immediately applicable if there is no time structure evidented or potentially assumed in the data. What I did was to supress the incorporation of any time series filter as I had domain knowledge/"knew" that it was captured in a cross-sectional i.e.non-longitudinal manner.
. Tsay's procedure actually iterativel checks each and every point for " statistical importance" and then selects the best point requiring adjustment. Time series solutions are immediately applicable if there is no time structure evidented or potentially assumed in the data. What I did was to supress the incorporation of any time series filter as I had domain knowledge/"knew" that it was captured in a cross-sectional i.e.non-longitudinal manner.








