4

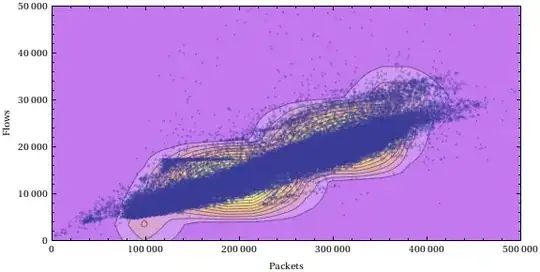
In my previous question I needed to help with ellipse region extraction and determine if point lies in that region or not. I ended up with this code:

library(ellipse)
library(mvtnorm)
require(spatstat)

netflow <- read.csv(file="data.csv",head=FALSE,sep=" ")
#add headers
names(netflow)<-c('timestamps','flows','flows_tcp','flows_udp','flows_icmp','flows_other','packe ts','packets_tcp','packets_udp','packets_icmp','packets_other','octets','octets_tcp','octets_udp','octets_icmp','octets_other')
attach(netflow)

#load library
library(sfsmisc)
#plot
plot(packets,flows,type='p',xlim=c(0,500000),ylim=c(0,50000),main="Dependence number of flows on number of packets",xlab="packets",ylab="flows",pch = 16, cex = .3,col="#0000ff22",xaxt="n")
#Complete the x axis
eaxis(1, padj=-0.5, cex.axis=0.8)

pktsFlows=subset(na.omit(netflow),select=c(packets,flows))
head(pktsFlows)
#plot(pktsFlows,pch = 16, cex = .3,col="#0000ff22")

cPktsFlows <- apply(pktsFlows, 2, mean)
elpPktsFlows=ellipse::ellipse(var(pktsFlows),centre=cPktsFlows,level=0.8)

png(file="graph.png")
plot(elpPktsFlows,type='l',xlim=c(0,500000), ylim=c(0,50000))
points(pktsFlows,pch = 19, cex = 0.5,col="#0000FF82")
grid(ny=10,nx=10)
dev.off()

W <- owin(poly=elpPktsFlows)
inside.owin(100000,18000,W)

This produces this graph.

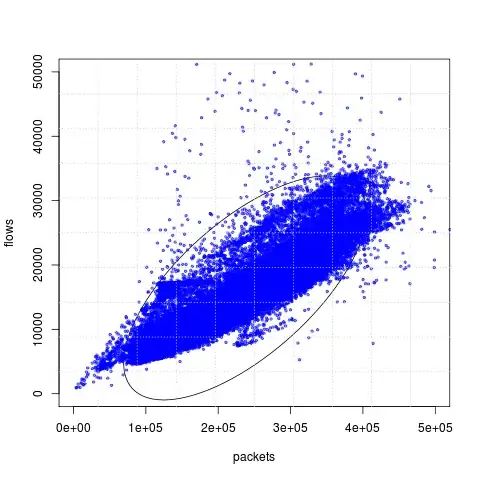
graph ellipse

Here is the same data with the regression line plotted

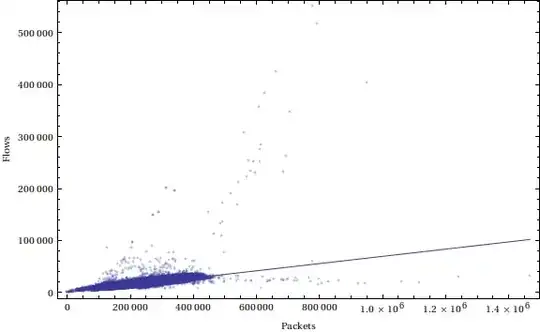Plot all with linear regression line.

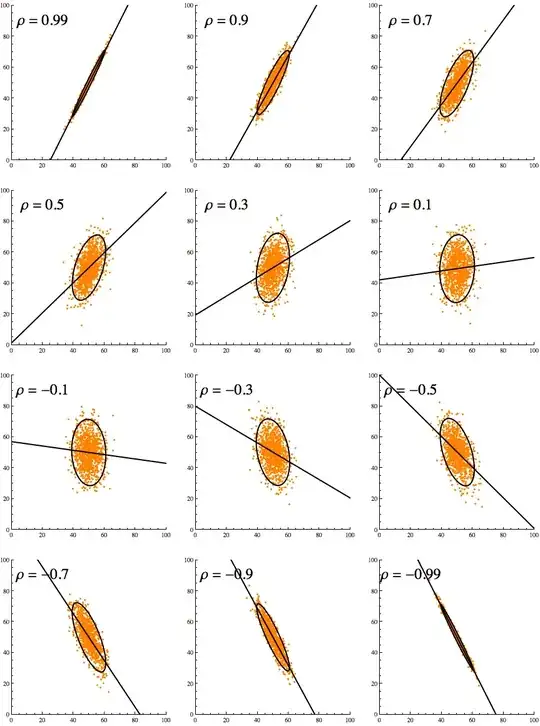
Can you explain me, why the ellipse has this shape? I expected that main axe of ellipse will have the same direction with linear regression line, but it hasn't.

Btw. kernel density estimation also points to 100000 althought there are no points...

kernel density estimation

Community
  • 1
matejuh
  • 315
  • 1
  • 2
  • 8
  • Please see the [markdown help](http://stats.stackexchange.com/editing-help) (you should have enough reputation to insert pictures into your post yourself now). I believe there are some other questions on this site that answer this question (or at least have pertinent discussion), see [Effect of switching response and explanatory variable in simple linear regression](http://stats.stackexchange.com/q/20553/1036) for one potentially helpful response. – Andy W Mar 13 '12 at 15:35
  • 1
    "I expected that main axe of ellipse will have the same direction with linear regression line, but it hasn't." This is a fundamental (but surprising) property of linear regression, called "regression to the mean." (Do a search on that phrase. :-) Unfortunately, I am unable to find any Web page containing a suitable illustration (in the form of a bivariate scatterplot)! Introductory stats textbooks do, however, explain this phenomenon copiously. – whuber Mar 13 '12 at 17:28

1 Answers1

11

Here you can see how the difference in orientation between the ellipse and the regression line changes depending on the correlation between x and y; higher is the correlation, closer is the agreement.

enter image description here

VLC
  • 379
  • 2
  • 6