2

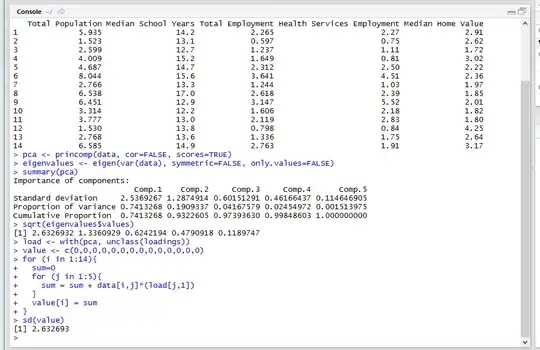
I am using the function princomp in R to run a principal components analysis.

In the summary() of the model, the standard deviations of the components are listed. However, these standard deviations are not the same as the square root of the eigenvalues. Shouldn't these values be the same?

In an attempt to figure out what was wrong, I also tried to take each observation and multiply each term by its respective coefficient in the first component and then summed them. I then took the standard deviation of all of these calculated values. The standard deviation from this method matched the square root of the eigenvalues.

Why is the standard deviation in the summary not matching the standard deviation I calculated by hand and the square root of the eigenvalues? Am I mistaken in believing they should be the same?

Here is the code:

#import Data
data <- T8.5
attach(data)

#name variables
names(data) <- c("Total Population", "Median School Years", "Total    Employment", "Health Services Employment", "Median Home Value")

#show data
data

#PCA
pca <- princomp(data, cor=FALSE, scores=TRUE)
eigenvalues <- eigen(var(data), symmetric=FALSE, only.values=FALSE)

#The standard deviations are different in the next two lines
summary(pca)
sqrt(eigenvalues$values)

#Here is where I tried to calculate the first component by hand
load <- with(pca, unclass(loadings))
value <- c(0,0,0,0,0,0,0,0,0,0,0,0,0,0)
#Testing the standard deviation for component 1
for (i in 1:14){
  sum=0
  for (j in 1:5){
    sum = sum + data[i,j]*(load[j,1])
  } 
  value[i] = sum
}
sd(value)
#This matches the sqrt(eigenvalues)

Here is the output I am getting in RStudio

amoeba
  • 93,463
  • 28
  • 275
  • 317
Jess B.
  • 21
  • 3
  • 1
    Can you paste in your output & some sample data? – gung - Reinstate Monica Oct 17 '16 at 00:02
  • 2
    Have you noticed that the ratios of the "Standard Deviation" line of your output and the square roots of the eigenvalues are all equal to $0.9636241 = \sqrt{13/14}$? – whuber Oct 18 '16 at 13:40
  • Do you mean the function `princomp` in the `stats` package? I don't see a package called princomp. `stats::princomp` has some defaults that may be surprising to you, depending on how you think about PCA. Try running your PCA using `principal` in the `psych` package instead, and check out the help documentation for `principal` for some discussion of the differences between `princomp` and `principal`. – Rose Hartman Oct 17 '16 at 04:56
  • 1
    @whuber Your comment (+1) reminded me that this is a duplicate. – amoeba Oct 18 '16 at 13:56

0 Answers0