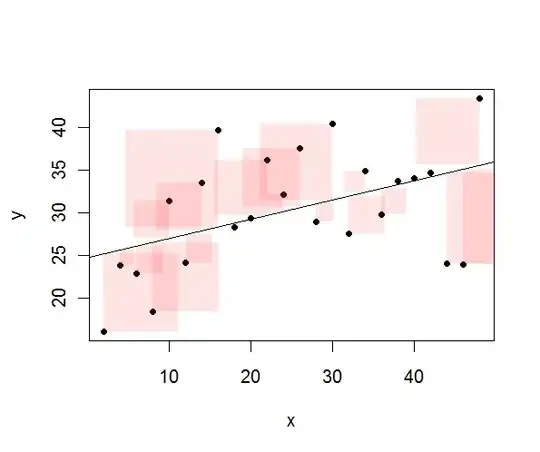
I came across this nice illustration of the "Coefficient of determination" (source):

Which leads me to ask two questions:
- How to do it with R? (I guess my main question would be how to deal with the opacity)
- Are there other interesting/useful visualizations of the "Coefficient of determination"? (and again, is there an easy way to make them in R?)
Thanks.