2

After many months of lurking, this is my first post (fingers crossed).

I have a 'large data' set (~ 5m observations of runs at UK parkrun events) to which I am trying to fit a multilevel model (because of repeated measures from specific runners over time) using R. Here is a quick summary of the variables I am working with:

Outcome: 5k run time (integer in minutes, e.g. 21.5)

Predictors: gender (two level factor); age (integer); previous runs (integer); friends present during run (integer); athlete number or athnumber (factor; level 2 random effect in the multilevel model)

Using lmer, I fit a model as follows:

model <- lmer(time ~ gender + age + runs + friends + (1 | athnumber), data = mydata)

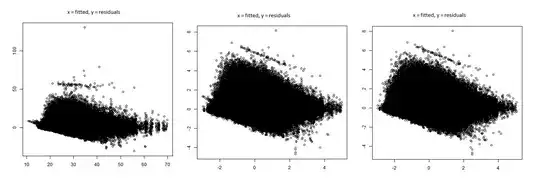
I am concerned with the fitted v. residuals plot that this model produces. With plot(fitted(model), resid(model)) I get the plot on the left below.

Using the same model, log transforming (and scaling) the time variable (which has a positive skew) does not seem to help, in fact it makes it worse (middle plot).

And I get a similar output (the plot on the right) again from the same model if I scale and log transform time, age and the positively skewed predictors (i.e., runs and friends):

enter image description here

For these plots: x = fitted, y = residuals (sorry they're small but I only get two images since I have less than 10 reputation points!)

I have also messed around with trimming the time variable and trimming the age variable, but, if anything, this just makes the fitted v. residual plots look more like diagonal rectangles (i.e., they become less fuzzy, but are still the same shape).

However, if I run a non-hierarchical linear model (with scaled and log transformed versions of time, runs, friends, and age) on a subset of the data obtained from randomly sampling one run from each athlete (thus removing the necessity of including athnumber in a multilevel model), I get a much more reasonable looking fitted v. residual plot. I get the following from model <- lm(time ~ gender + age + runs + friends, mydata) and plot(fitted(model), resid(model)):

enter image description here

So, the lm() seems okay in this regard. But the way I understand it, the multilevel model is predicting time scores that are too fast (positive residuals) for fast runs and time scores that are too slow (negative residuals) for slow runs, is this correct?

So, my questions are: (1) why am I getting this strange-looking fitted v. residual plot for the multilevel model? And (2) surely this means the model is biased and makes any inference invalid, correct? And (3) how can I fix this problem?

Thanks very much for the help and understanding in advance - I'm self-taught with this stuff so please forgive any mistakes. Cheers!

arranjdavis
  • 146
  • 6
  • The correct `lmer` syntax is `model – Roland Sep 05 '16 at 09:12
  • One problem is that times cannot be below zero. The log transformation is an attempt to solve this, but it can't be effective if all values are rather far from zero and not very spread out compared to the distance from zero. That's usually the case for running times. You could try other transformations or a glmm. You also need to consider random slopes (e.g., for age since some individuals develop faster than others), interactions (girls develop faster than boys), non-linearities (usually there is an optimum age). The latter you could model with a GAMM (see package mgcv). – Roland Sep 05 '16 at 09:26
  • Adding to the comment of @Roland, note that the relation residual = observed $-$ fitted yields a bounding line residual = $-$ fitted for observed = 0. So, it's impossible to populate every corner of this space. – Nick Cox Sep 05 '16 at 11:37
  • BTW, I think it's a little more common to refer to this as a residual vs fitted plot. If this point seems of interest, http://stats.stackexchange.com/questions/146533/versus-vs-how-to-properly-use-this-word-in-data-analysis is a longer discussion. – Nick Cox Sep 05 '16 at 11:39
  • Hi @Roland, thanks for engaging with this! Sorry about the typo, I've corrected it now. I agree that adding random effects would be helpful, but I want to fit a more basic model first because when I add random effects (of age or the combinations of runs and friends) I still get residual v. fitted plots with similar patterns, which suggests, to me at least, that these models aren't fitting the data very well (also, adding these random effects produce warnings about 'very large eigenvalues and nearly unidentifiable models'). – arranjdavis Sep 05 '16 at 12:33
  • re modelling ranks: No. – Roland Sep 05 '16 at 14:04

0 Answers0