Check the following code to better understand my comment above.
When you feed a date independent variable to a model you let R transform it to a number which messes up your interpretation.
If you transform your variable to distance from first measurement (in minutes) you know exactly what you're trying to interpret.
structure(list(TimePeriod = structure(c(1464926400, 1464927300,
1464928200, 1464929100, 1464930000, 1464930900, 1464931800, 1464932700,
1464933600, 1464934500), class = c("POSIXct", "POSIXt"), tzone = ""),
cpubusy = c(35.66, 37.05, 36.9, 36.66, 37.51, 37.2, 35.26,
36.81, 36.14, 36.18)), .Names = c("TimePeriod", "cpubusy"
), row.names = c(NA, 10L), class = "data.frame") -> dt
dt$TimePeriod2 = seq(0,9)*15
dt$TimePeriod3 = as.numeric(dt$TimePeriod)
dt
# TimePeriod cpubusy TimePeriod2 TimePeriod3
# 1 2016-06-03 05:00:00 35.66 0 1464926400
# 2 2016-06-03 05:15:00 37.05 15 1464927300
# 3 2016-06-03 05:30:00 36.90 30 1464928200
# 4 2016-06-03 05:45:00 36.66 45 1464929100
# 5 2016-06-03 06:00:00 37.51 60 1464930000
# 6 2016-06-03 06:15:00 37.20 75 1464930900
# 7 2016-06-03 06:30:00 35.26 90 1464931800
# 8 2016-06-03 06:45:00 36.81 105 1464932700
# 9 2016-06-03 07:00:00 36.14 120 1464933600
# 10 2016-06-03 07:15:00 36.18 135 1464934500
lin<-lm(data=dt, cpubusy~TimePeriod)
summary(lin)
# Call:
# lm(formula = cpubusy ~ TimePeriod, data = dt)
#
# Residuals:
# Min 1Q Median 3Q Max
# -1.2166 -0.2359 0.1624 0.3733 0.9528
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 6.564e+04 1.332e+05 0.493 0.635
# TimePeriod -4.478e-05 9.095e-05 -0.492 0.636
#
# Residual standard error: 0.7435 on 8 degrees of freedom
# Multiple R-squared: 0.02941, Adjusted R-squared: -0.09191
# F-statistic: 0.2424 on 1 and 8 DF, p-value: 0.6357
lin<-lm(data=dt, cpubusy~TimePeriod2)
summary(lin)
# Call:
# lm(formula = cpubusy ~ TimePeriod2, data = dt)
#
# Residuals:
# Min 1Q Median 3Q Max
# -1.2166 -0.2359 0.1624 0.3733 0.9528
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 36.718364 0.436968 84.030 4.49e-13 ***
# TimePeriod2 -0.002687 0.005457 -0.492 0.636
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 0.7435 on 8 degrees of freedom
# Multiple R-squared: 0.02941, Adjusted R-squared: -0.09191
# F-statistic: 0.2424 on 1 and 8 DF, p-value: 0.6357
lin<-lm(data=dt, cpubusy~TimePeriod3)
summary(lin)
# Call:
# lm(formula = cpubusy ~ TimePeriod3, data = dt)
#
# Residuals:
# Min 1Q Median 3Q Max
# -1.2166 -0.2359 0.1624 0.3733 0.9528
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 6.564e+04 1.332e+05 0.493 0.635
# TimePeriod3 -4.478e-05 9.095e-05 -0.492 0.636
#
# Residual standard error: 0.7435 on 8 degrees of freedom
# Multiple R-squared: 0.02941, Adjusted R-squared: -0.09191
# F-statistic: 0.2424 on 1 and 8 DF, p-value: 0.6357
Model 1 and 3 are the same because that's what R does to your date variable in order to produce coefficients.
2nd model has same predictive capability, as expected, because you haven't changed your variable. You just transformed it to something more meaningful to you.
If you follow the approach of the 2nd model you know your variable is expressed in minutes. The coefficient obtained by the model, let's say C (positive), is your growth rate. And you can say that on average your dependent variable increases by C for every minute. Or C * 60 per hour, etc.
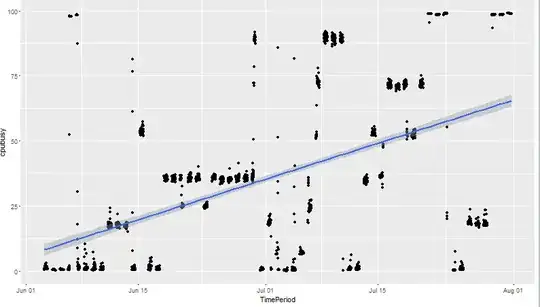 I have a time series data like this:
I have a time series data like this: