Why does ecdf uses a step function and not a linear interpolation?

Question

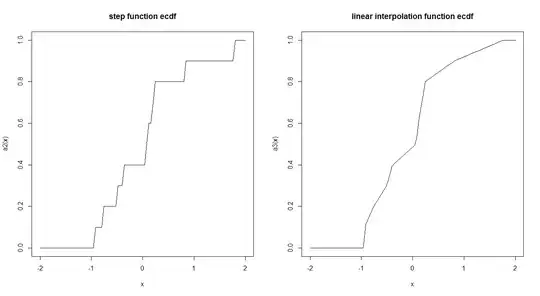
Empirical CDF functions are usually estimated by a step function. Is there a reason why this is done in such a way and not by using a linear interpolation? Does the step function has any interesting theoretical properties which make us prefer it?

Here is an example of the two:

ecdf2 <- function (x) {
  x <- sort(x)
  n <- length(x)
  if (n < 1) 
    stop("'x' must have 1 or more non-missing values")
  vals <- unique(x)
  rval <- approxfun(vals, cumsum(tabulate(match(x, vals)))/n, 
                    method = "linear", yleft = 0, yright = 1, f = 0, ties = "ordered")
  class(rval) <- c("ecdf", class(rval))
  assign("nobs", n, envir = environment(rval))
  attr(rval, "call") <- sys.call()
  rval
}


set.seed(2016-08-18)
a <- rnorm(10)
a2 <- ecdf(a)
a3 <- ecdf2(a)

par(mfrow = c(1,2))
curve(a2, -2,2, main = "step function ecdf")
curve(a3, -2,2, main = "linear interpolation function ecdf")

[Related](http://uk.mathworks.com/help/stats/examples/nonparametric-estimates-of-cumulative-distribution-functions-and-their-inverses.html?requestedDomain=www.mathworks.com)................................... — , Aug 18 '16 at 12:48
"...estimated by a step function" belies a subtle misconception: the ECDF is not merely *estimated* by a step function; it *is* such a function by definition. It is identical to the CDF of a random variable. Specifically, given any finite sequence of numbers $x_1, x_2, \ldots, x_n$, define a probability space $(\Omega,\mathfrak{S},\mathbb{P})$ with $\Omega=\{1,2,\ldots, n\}$, $\mathfrak{S}$ discrete, and $\mathbb{P}$ uniform. Let $X$ be the random variable assigning $x_i$ to $i$. *The ECDF is the CDF of $X$.* This enormous conceptual simplification is a compelling argument for the definition. — whuber, Aug 18 '16 at 13:52

score 22 · Accepted Answer · edited Aug 18 '16 at 16:00

22

It's by definition.

The empirical distribution function of a set of observations $(X_n)$ is defined by

$$F_e(t) = \frac{\#\{X_n \mid X_n \le t\}}n$$

Where $\#$ is the set cardinality. This is, by nature, a step function. It converges to the actual CDF almost surely.

Also note that for any distribution with $P(X = x) \ne 0$ for at least two $x$ (especially nondegenerate discrete distributions), your variant of ECDF does not converge to the actual CDF. For example consider a Bernoulli distribution with CDF

$$F_X(x) = p \chi_{x \ge 0} + (1-p) \chi_{x \ge 1}$$ this is a step function whereas ecdf2 will converge to $\chi_{x\ge 0} \cdot (p + (1-p)\min(x, 1))$ (a piecewise linear function connecting $(0,p)$ and $(1,1)$.

edited Aug 18 '16 at 16:00

Will Vousden

186
6

answered Aug 18 '16 at 10:10

AlexR

739
4
12

Thanks Alex. So is there another name for the function I wrote? (because I would guess it also converges to the actual CDF) – Tal Galili Aug 18 '16 at 10:19
5

@TalGalili It doesn't. Consider a Bernoulli distribution. Your ecdf2 will not converge in this case. You could call it a smoothed ecdf. I suspect it will converge to the actual CDF iff the actual CDF has no points with nonzero probability except for extreme points (where you don't smooth) – AlexR Aug 18 '16 at 11:02
@AlexR you could edit your answer to add this comment since discrete distributions are *the reason* for such definite -- so it answers the "why" question. – Tim Aug 18 '16 at 13:02
1

@Tim Done. ${}{}$ – AlexR Aug 18 '16 at 14:33
Thanks. Is there a way to define a continuous empirical function that would converge to the step function but would be fully monotone (i.e.: without any sharp "jumps")? – Tal Galili Aug 19 '16 at 10:02
@TalGalili Yes, smooth the ECDF with a (smooth) kernel family (aka mollifier) by convolution. Increase the family index (decrease the smoothness of the kernel) as the number of observations increases. The resulting estimate is $C^\infty$ at all times and converges almost surely to the CDF. – AlexR Aug 19 '16 at 15:58
Hi Alex - (1) thanks. (2) could you give me an example of such a solution? (preferably in R :) ) – Tal Galili Aug 19 '16 at 23:22
(I approved your great answer - but would still appreciate help with my followup question) Thanks! – Tal Galili Aug 21 '16 at 18:38
@TalGalili I'll think about it when I have time. But thanks so far :) – AlexR Aug 21 '16 at 19:02
What if you assume the true distribution is continuous? – user76284 Oct 13 '19 at 03:49
@user76284 Continuous distributions have a continuous ECDF, so that will work. – AlexR Oct 15 '19 at 04:58
What would be the analogue if you know you have a continuous *density*? In that case, the smoothed empirical CDF has to be differentiable, not just continuous (piecewise linear). – user76284 Oct 15 '19 at 05:10
@user76284 Analogue to what? You could use spline interpolation of any order to get any continuity level of the interpolation function. Or mollify the real ecdf as suggested in my answer for a $C^\infty$ interpolation. – AlexR Oct 15 '19 at 05:26
@AlexR I guess what I'm asking is what would be the most "principled" such interpolation. In what sense can one such interpolation be "better" than another? Perhaps it converges faster to the true CDF, in the limit of infinite samples? For example, linear interpolation is (I think) minimizing the [total variation](https://en.wikipedia.org/wiki/Total_variation) of the result subject to the constraint that it matches the sampled values. Should we now just add the constraint of differentiability to this variational problem? – user76284 Oct 15 '19 at 15:56
Actually, I think adding the constraint of differentiability just leads to a sequence of differentiable solutions that get arbitrarily closer to the linear interpolation (i.e. with smaller and smaller "bends" at the sampled points), so there is no optimum. Perhaps a different variational problem or more constraints are needed. – user76284 Oct 15 '19 at 16:03

Why does ecdf uses a step function and not a linear interpolation?

1 Answers1