R using GLM and manual solve logistic regression have different (close but not exactly the same) results

Question

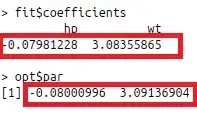
I am getting different results (close but not exact the same) from R GLM and manual solving logistic regression optimization. Could anyone tell me where is the problem?

BFGS does not converge? Numerical problem with finite precision?

Thanks

# logistic regression without intercept
fit=glm(factor(vs) ~ hp+wt-1, mtcars, family=binomial())

# manually write logistic loss and use BFGS to solve
x=as.matrix(mtcars[,c(4,6)])
y=ifelse(mtcars$vs==1,1,-1)

lossLogistic <- function(w){
  L=log(1+exp(-y*(x %*% w)))
  return(sum(L))
}

opt=optim(c(1,1),lossLogistic, method="BFGS")

@MatthewDrury Thanks. You expect the `optim` does not converge? — Haitao Du, Aug 14 '16 at 02:09
No, it should converge, the logistic loss in convex. But maybe the default tolerance for `glm` is tighter than that for `optim`. — Matthew Drury, Aug 14 '16 at 02:15
diff by 0.001 is higher than what I expected. `control = list(maxit = 1e8, abstol=1e-8, reltol=1e-8)` still not help. — Haitao Du, Aug 14 '16 at 02:19
I suspect it is finite precision problem, `mtcars$hp` is several hundred, may be after `exp`, there are problems... — Haitao Du, Aug 14 '16 at 02:59
just tried. seems no. I found the BFGS results seems have something to do with the initial value. So, may be not converge. and function `nlm` is returning another similar but not exact the same value. — Haitao Du, Aug 14 '16 at 03:36
@MatthewDrury: Good idea about standardising the data but unfortunately not quite what went wrong here! — usεr11852, Aug 14 '16 at 08:21

usεr11852 · Accepted Answer · 2016-08-14T17:38:47.060

7

Short answer: Optimise harder.

Your loss function is fine, no numeric issues there. For instance you can easily check that:

all.equal( lossLogistic(coef(fit)), as.numeric(-logLik(fit)), 
           check.attributes = FALSE)
[1] TRUE

What happens is that you assume that optim's BFGS implementation can get as good as an routine that use actual gradient information - remember Fisher scoring is essentially a Newton-Raphson routine. BFGS converged ( opt$convergence equals 0) but the best of BFGS was not the best you could get because as you did not provide a gradient function the routine had to numerically approximate the gradient. If you used a better optimisation procedure that could use more gradient-like information you would get the same results. Here, because the log-likelihood is actually a very well behaved function I can even use a quadratic approximation procedure to "fake" gradient information.

library(minqa)
optQ= minqa::uobyqa(c(1,1),lossLogistic)
all.equal( optQ$par, coef(fit), check.attributes = FALSE)
[1] TRUE
all.equal( optQ$fval, as.numeric(-logLik(fit)), 
           check.attributes = FALSE)
[1] TRUE

It works.

edited Aug 14 '16 at 17:38

answered Aug 14 '16 at 07:50

usεr11852

33,608
2
75
117

Thank you very much for the great answer. I also learned `minqa` from you! – Haitao Du Aug 14 '16 at 12:21
Hmmm. I had it in my brain that BFGS *requires* a gradient as input. Does it work out some approximation if you don't supply it? – Matthew Drury Aug 14 '16 at 16:19
1

BFGS does require gradient information but this information will be numerically approximated when not provided to `optim`. To quote `optim`'s doc: "*If (grad) is NULL, a finite-difference approximation will be used.*" I checked the code in [optim.c](https://github.com/wch/r-source/blob/trunk/src/library/stats/src/optim.c) where the finite differences are computed; it is a standard first-order centred difference scheme. Nice for something quick and dirty but clearly no match for a quadratic approximation routine. – usεr11852 Aug 14 '16 at 17:08
@hxd1011: I learned about it reading through the `R-sig-ME` e-mail list (`ME` stands for mixed effects). It was one of the major things that changed between the 0.999... and the 1.x-y versions of `lme4`. It started offering `bobyqa` and `Nelder-Mead` as optimisation options; this was quite contrary to the approach of `lme` where it used a combination of E-M steps followed by N-R iterations. – usεr11852 Aug 14 '16 at 17:24
@MatthewDrury: Thanks for pointing out the ambiguity regarding the current use of gradient information by `optim`'s BFGS. I hope the minor edit and the comment following your observation clear out things more. – usεr11852 Aug 14 '16 at 17:40
2 years later, I learned details about glm in [this great answer](https://stats.stackexchange.com/questions/344309/why-using-newtons-method-for-logistic-regression-optimization-is-called-iterati)! – Haitao Du May 07 '18 at 20:01

R using GLM and manual solve logistic regression have different (close but not exactly the same) results

1 Answers1

Linked