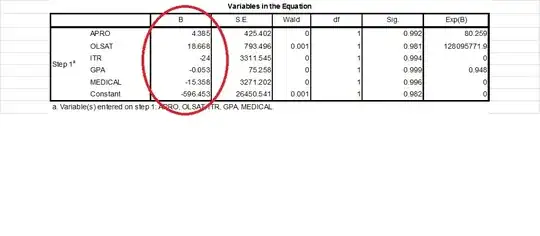
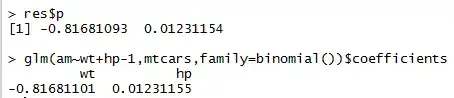
I am doing a study about logistic regression. I have to write a program for the admission process of the school. The result is passed or failed.
Logit = L = b0 + b1X1 + b2X2 + …+ bkXk ...
What is the formula for b0, b1, b2, b3 (i.e., the beta coefficients) that can be seen at the picture? What is the formula for the raw coefficient for logistic regression?