1

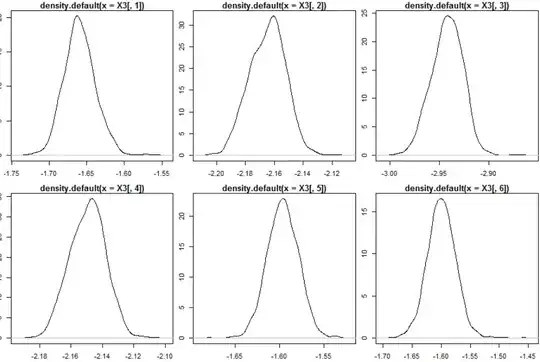
We want to apply PCA to monitor our process testing data. After we plot the density of the testing data and do normality tests, we found them to be definitely not normal, but still symmetrical and long tailed.

What distribution can these be?

If they are not normal, is PCA still be applicable? If not, what other monitoring technique could be used?

We have too many of those testing data, so eyeballing them 1 by 1 is definitely not a good choice.

enter image description here

shapiro test
  ARM_Z  RAMP_Z  DISC_Z RAMP_Z8  ARM_Z1  ARM_Z2 
 0.0000  0.0032  0.0000  0.0724  0.0246  0.0000 

adf test
  ARM_Z  RAMP_Z  DISC_Z RAMP_Z8  ARM_Z1  ARM_Z2 
   0.01    0.01    0.01    0.01    0.01    0.01 

jarque-bera test
  ARM_Z.X-squared  RAMP_Z.X-squared  DISC_Z.X-squared RAMP_Z8.X-squared  ARM_Z1.X-squared  ARM_Z2.X-squared 
           0.0000            0.4580            0.0003            0.8591            0.0029            0.0000

They are more peaked than corresponding fitted normal distributions.

amoeba
  • 93,463
  • 28
  • 275
  • 317
John
  • 263
  • 2
  • 12
  • 4
    What makes you consider those distributions "definitely not normal" and "long tailed"?! You *rarely* as bell-curved shapes as yours in real-life data! See also: http://stats.stackexchange.com/questions/2492/is-normality-testing-essentially-useless – Tim Aug 11 '16 at 09:28

1 Answers1

2

PCA analysis takes into consideration only the first two moments of the (joint) distribution of the multivariate random variables. In fact the procedure relies on the definition of an Euclidean metric to measure distance between random distributions. If the underlying distributions are normal, then the analysis takes into consideration ALL the information available, as a multivariate normal distribution is described solely and uniquely by its mean and variance-covariance matrix. If the underlying distribution is NOT normal, conversely, you are, so to speak, ignoring information by applying a mean-variance method. For practical purposes, however, if the distributions are not too pathological (and your marginals do not seem so) PCA can still be reliably applied to obtain information about the statistical dependence of the different components. The only thing you have to remember, is that this characterization is not COMPLETE, in the sense that there could be some dependence in the higher moments of the variables that the variance analysis is not able to capture.

g1ul10
  • 96
  • 2