Role of Dirac function in particle filters

Question

Particle approximations to probability densities are often introduced as a weighted sum of Dirac functions

$$p(x) \approx \sum_{i=1}^N \omega^i \delta(x-x^i)$$

with the weights

$$\omega^i \propto \frac{p(x^i)}{q(x^i)}$$

normalized such that they sum to unity; where $q(\cdot)$ is the importance density. I understand that the Dirac function becomes infinitely large at a point $p$, that is $\delta(p) = \infty$ and that it is zero elsewhere, that is $\delta(x) = 0 ~\forall x \neq p$. Also, I understand that the Dirac function integrated over the mass point takes the value of unity.

My questions are:

1. What is the relationship between the support of the particle approximation and the Dirac function?
2. Why is a summation sign used when evaluating $\delta$ can only ever yield a value of 0 or infinity? Shouldn't this be an integral instead?
3. How can the notion of the support of a function be extended to a set of points (e.g., $x_t^{(i)}$), which isn't itself a function?
4. How can a representation of a probability density function arise from a weighted sum of $\delta(\cdot)$s that themselves take only values of either zero or infinity?

Thank you for any clarifications you may be able to provide.

Answer 1

@user20160 has already given you nice answer to your (1)-(3) questions, but the last one seems to be not yet fully answered.

4. How can a representation of a probability density function arise from a weighted sum of $\delta(\cdot)$s that themselves take only values of either zero or infinity?

Let me start with quoting Wikipedia as it provides a pretty clear description in this case (notice the bolds I added):

The Dirac delta can be loosely thought of as a function on the real line which is zero everywhere except at the origin, where it is infinite,

$$\delta(x) = \begin{cases} +\infty, & x = 0 \\ 0, & x \ne 0 \end{cases}$$

and which is also constrained to satisfy the identity

$$\int_{-\infty}^\infty \delta(x) \, dx = 1$$

This is merely a heuristic characterization. The Dirac delta is not a function in the traditional sense as no function defined on the real numbers has these properties. The Dirac delta function can be rigorously defined either as a distribution or as a measure.

Further on, Wikipedia provides more formal definition and lots of worked examples, so I'd recommend you go through the whole article. Let me quote one example from it:

In probability theory and statistics, the Dirac delta function is often used to represent a discrete distribution, or a partially discrete, partially continuous distribution, using a probability density function (which is normally used to represent fully continuous distributions). For example, the probability density function $f(x)$ of a discrete distribution consisting of points $x = \{x_1, \dots, x_n\}$, with corresponding probabilities $p_1, \dots, p_n$, can be written as

$$ f(x) = \sum_{i=1}^n p_i \delta(x-x_i) $$

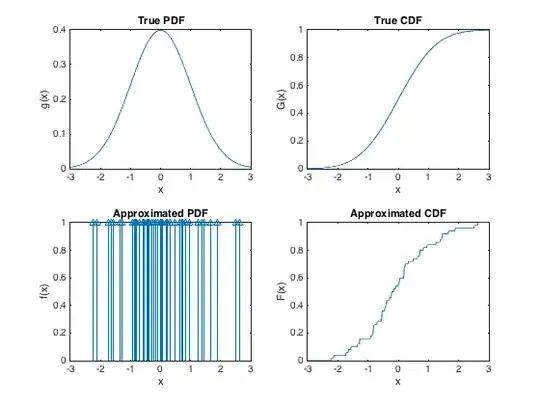
What this equation is saying is that we take sum over $n$ continuous distributions $\delta_{x_i} = \delta(x-x_i)$ that have all their mass around $x_i$'s. If you'd try to imagine $\delta_{x_i}$ distributions in terms of cumulative distribution functions, it needs to be

$$ F_{x_i}(x) = \begin{cases} 0 & \text{if } x < x_i \\ 1 & \text{if } x \ge x_i \end{cases} $$

So we can re-write previous density to cumulative distribution function

$$ F(x) = \sum_{i=1}^n p_i F_{x_i}(x) = \sum_{i=1}^n p_i \mathbf{1}_{x \ge x_i} $$

where $\mathbf{1}_{x \ge x_i}$ is an indicator function pointing at $x_i$. Notice that this basically is a categorical distribution in disguise. Moreover, you can define Dirac delta in terms of arbitrary function

$$ \int_{-\infty}^\infty f(x) \delta(x-x_i) dx = f(x_i) $$

so it "works" as continuous version of indicator function.

The take-away message is that Dirac delta is not a standard function. It's also not equal to infinity at zero -- if it was, it would be useless because infinity is not a number, so we couldn't perform any arithmetic operations over it. You can think of Dirac delta simply as an indicator function pointing at some $x_i$ that is continuous and integrates to unity. No black magic involved, it is just a way to hack the calculus to deal with discrete values.

Answer 2

What is the relationship between the support of the particle approximation and the Dirac function?

The distribution is approximated as a weighted sum of delta functions. So, the support of the approximation is the the union of the support of the delta functions. Each delta function is zero everywhere except for a single point ($x_t^{(i)}$), where its value is infinite. So, the support of each delta function is that single point, and the support of the approximating distribution is the set of points $\left \{ x_t^{(i)} \right \}_{i=1}^N$

Why is a summation sign used when evaluating $\delta$ can only ever yield a value of 0 or infinity? Shouldn't this be an integral instead?

The sum is there to express the distribution as a weighted sum of delta functions. This is just saying: "place a delta function at each point $x_t^{(i)}$, and scale its amplitude by $\pi_t^{(i)}$." The distribution is continuous, so its value at each point is the probability density, not the probability. We'd integrate the density over some region to get the associated probability. The integral of each scaled delta function will be $\pi_t^{(i)}$. This means the probability of each point $x_t^{(i)}$ is $\pi_t{(i)}$, and the probability of any other value is 0.

Here's an example of approximating a continuous distribution using delta functions. The distribution $g$ is a Gaussian distribution. $g$ is approximated using distribution $f$, which is a sum of 50 scaled delta functions. The locations of the delta functions are sampled from $g$.

By eye, the PDFs don't look very similar because $f$ doesn't have a nice shape that we can see. But, the delta functions are packed closer together in regions where $g$ has higher density. Once we start taking integrals, the similarity becomes more apparent. For example, the CDFs are noticeably similar. The mean, variance, etc. will also be similar. The quality of the approximation will improve as the number of samples/delta functions increases.

How can the notion of the support of a function be extended to a set of points (e.g., $x^{(i)}_t$), which isn't itself a function?

Support is a concept defined for functions, not sets. The support of a function is the set of inputs for which the output is nonzero. As above, if we define a function as a sum of delta functions located at each point in a set $S$, the support of that function is $S$. We can also consider the indicator function of $S$. Say $S$ is a subset of some larger set $L$ (e.g. the real numbers). The indicator function $I_S(x)$ is defined on $L$. It takes a value of $1$ if $x \in S$, otherwise $0$. So, the support of the indicator function is $S$.

Answer 3

How can a representation of a probability density function arise from a weighted sum of δ(⋅)s that themselves take only values of either zero or infinity?

Think of Dirac's delta function as a bridge between discrete and continuous values. Dirac came up with them to simplify his math by applying continuous math tools to discrete quantities. I think of Dirac's delta in precisely the same situations when it's too cumbersome to deal with discrete values.

So, in your example someone wanted to have the probability density function. Great! But the trouble is that your inputs are discrete observations. So, this dude knew about Dirac's function, and plugged it in:

$$p(x) \approx \sum_{i=1}^N \omega^i \delta(x-x^i)$$

To understand this expression bear in mind how Dirac's delta is defined: $$\int f(x)\delta(x-x_0)dx=f(x_0)$$ $$\delta(x)\equiv 0, \forall x\ne 0 $$

Notice, that it's not defined the way you described it:

Dirac function becomes infinitely large at a point pp, that is δ(p)=∞ and that it is zero elsewhere,

This is not the right way to think of a Dirac function. Always think of it as an integral above whose purpose is to link discrete value at $x_0$ to continuous expression (integral) $\int \dots dx$.

Now, apply an integral to your equation: $$\int p(x) dx \approx \int \left(\sum_{i=1}^N \omega^i \delta(x-x^i)\right) dx= \sum_i\omega_i$$

If you didn't have the Dirac' delta and applied the integral to a sum you'd get an undefined integral: $$\int \left(\sum_{i=1}^N \omega^i \right) dx=\infty$$

Summarizing, Dirac's delta purpose is bring discrete quantities into continuous space, and you definition of $p(x)$ demonstrates just that. It constructs the continuous density function out of $N$ discrete values.

Again, it is misleading to think of Dirac function as "infinity at $x_0$ and zero everywhere". This description does not bring anything useful in terms of intuition. Drop it.

Here's how Diract himself defined his function in "The Principles of Quantum Mechanics" :

This is how he describes the purpose of the function, notice how he keeps repeating the word "integrand" and emphasizes "convenience":

Answer 4

I think your confusions are all a result of thinking of the Dirac delta as a function. It is not (see wikipedia article https://en.wikipedia.org/wiki/Dirac_delta_function).

The delta function only makes sense as a mathematical object when it appears inside an integral. From this perspective the Dirac delta can usually be manipulated as though it were a function.

As @Tim quoted, the Dirac delta function can be rigorously defined either as a distribution or as a measure.

This is merely a heuristic characterization. The Dirac delta is not a function in the traditional sense as no function defined on the real numbers has these properties. The Dirac delta function can be rigorously defined either as a distribution or as a measure.

I think its easier to think of it as a measure ( ie essentially something you integrate against). So given a function f,

$\mu(f):= \int_{-\infty}^{\infty} f(x) \ d\mu(x)$

if you have a density p(x) then this induces a measure $P$:

$P(f)= \int_{-\infty}^{\infty} f (x)\ p(x)dx$

and the delta function induces a measure $\nu$ such that $\nu(f)=f(0)$

So the function notation just helps with eg adding measures together (Q2). ie what it's really saying is : $\mu(f):= \sum_{i=1}^{n} \nu_{x_i}(f)$ where

$\nu_{x_i}(f)=f(x_i)$

This viewpoint clarifies the support question too. the support is defined using arbitrary functions: all functions f without support at zero will have $\mu(f)$ = 0 Support of a distribution

As mentioned in the wikipedia article, the delta function can be viewed constructively as a limit of measures induced by Gaussians with mean at zero and vanishing standard deviation ($\sigma$) ( denoting Gaussian pdf as $g(x;\mu;\sigma)$ )

$\nu(f) = \lim_{\sigma\rightarrow 0} \int ^\infty _{-\infty} f(x) g(x;0,\sigma) dx$