I have fit two models on a count variable.
The first model is based on the assumption that the response variable is Poisson and the other is based on the assumption it is a negative binomial.
The AIC for the model where a Poisson family is assumed is 476497, whereas the AIC for the negative binomial assumption is 339581. Furthermore, the data has a large number of 0s and the mean of the count variable (response) is 1.974 while the variance is 12.86011 breaking the Poisson mean = variance assumption.
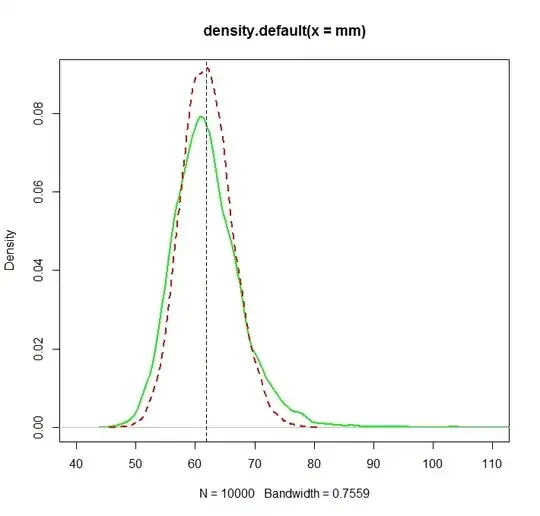
However, Micheal Friendly's distplot in R suggests the count variable follows a Poisson process. (Micheal Friendly's plot is essentially an equivalent form of the Q-Q plot for discrete data. It is interpreted in an identical manor as a Q-Q plot)
Which distribution should be applied to the glm?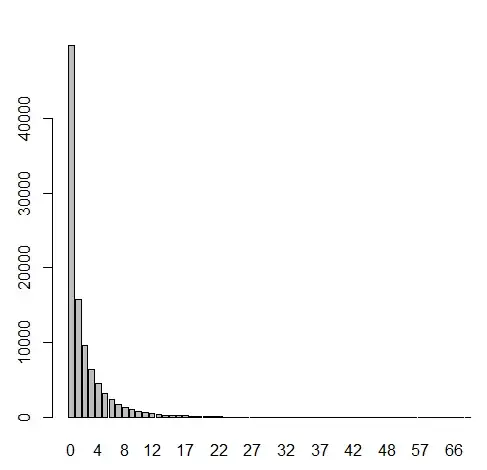
Lastly, I could fit a quasipoisson model but the AIC appears as NA for the model and I do not know any methods of testing a quasipoisson assumption so I do not know how to compare that model with these ones.
Thank you for your input.