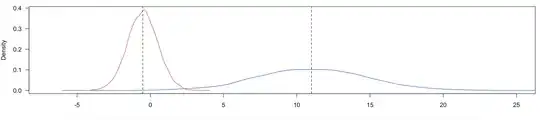
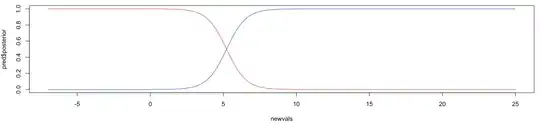
I have two normal distributions fg and bg with mean (mu) and standard deviations (sd) as follows:
set.seed(100)
fg = rnorm(10000, mean=11.00, sd=3.77)
bg = rnorm(10000, mean=-0.508, sd=1.04)
If I fit an LDA model like this:
library(MASS)
mydata = data.frame(label = c(rep(1, 10000), rep(0,10000)),
score = c(fg, bg))
fit = lda(label~score, data=mydata)
And try and to predict some new values:
newvals = seq(-7, 25, 0.1)
pred = predict(fit, data.frame(score=newvals))
# Plot posterior
matplot(newvals, pred$posterior, type='l', col=c('red', 'blue'), lty=1)
I get posteriors which look like this:
At a value of 5, the posterior for belonging to either class is 0.5, but looking at the density plots above, you can see that at 5 it almost always belongs to the fg distribution. I would expect the posterior to be 0.5 closer to 2.5-3, where both density curves cross eachother.
Can anyone please explain why the lda posteriors are behaving this way - or if I'm doing something wrong?
Thanks!