2

How should I derive a PDF from the difference of a couple of given two parameter Weibull distributions ? The convolution integrals become very difficult to evaluate. PS : The parameters are not necessarily the same since the idea is to get a distribution for a general case.

Sanket Doshi
  • 21
  • 2
  • please add more information to clarify your question – Antoine Jun 15 '16 at 11:49
  • Do they have the same values of their parameters or not? – whuber Jun 15 '16 at 12:13
  • Since we're considering a general case, it'll be better to assume that they do not have the same parameters. However, I don' think it'll make much difference since the convolution integral is equally difficult to compute. – Sanket Doshi Jun 15 '16 at 12:20
  • It makes a profound difference! When either both shape parameters are equal and equal to certain special values (such as $1$ or $2$), or both scale parameters are the same, a closed form answer is possible. Otherwise it does look difficult. – whuber Jun 15 '16 at 12:37
  • I am sorry. Your argument sounds correct. It looks tough to get a closed form solution in other cases. – Sanket Doshi Jun 15 '16 at 18:28

1 Answers1

2

This seems to be a difficult question. I tried to find a closed form answer with the help of maple, but maple gives up! So I will use the same numerical approach as used in Difference of two i.i.d. lognormal random variables. The convolution formulas used are developed there, so will not be redone here. If $X, Y$ are independent weibull distributed (possibly with different parameters) then the density of $D=X-Y$ is $$ f_D(t) = \int_0^\infty f(t+y) g(y) \; dy $$ with $f$ the density of $X$, $g$ the density of $Y$.

The density of the difference $D$ can then be calculated via numerical integration:

dDIFF <-  function(x, shape1, shape2=shape1, scale1=1, scale2=scale1) {
    res  <- x
    for (xx in seq(along=x)) {
        res[xx]  <-  integrate(function(y) dweibull(y+x[xx], shape1, scale1) * dweibull(y, shape2, scale2),  lower=0.0,  upper=+Inf)$value
    }
    return(res)
    }

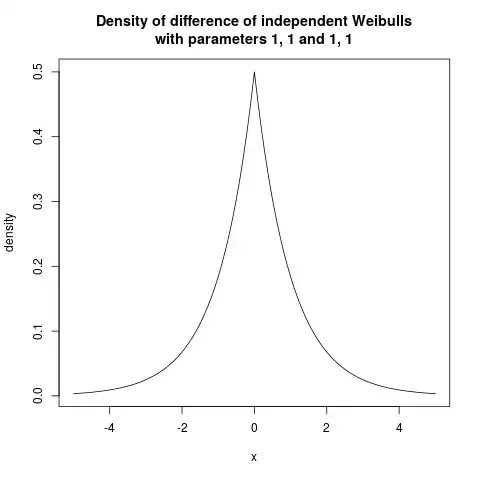
and we can make a plot of that, first in a symmetrical case:

plot of density by numerical integration, symmetric case

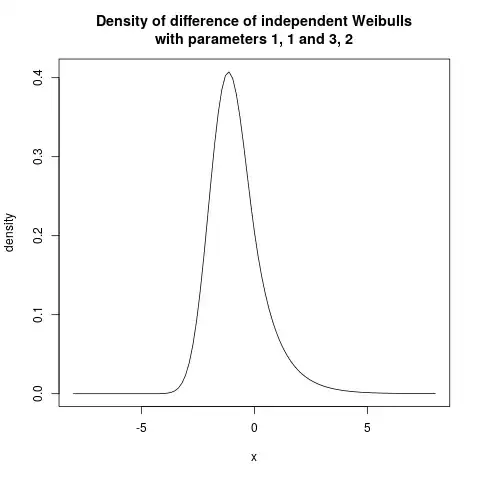
(note the cusp at zero), and then an asymmetrical case:

plot of density by numerical integration, asymmetrical case

This numerical solution is very fast and should be enough for most practical purposes! If you have to evaluate it very often, maybe make a spline approximation?

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467