Difference between gaussian and lognormal

Question

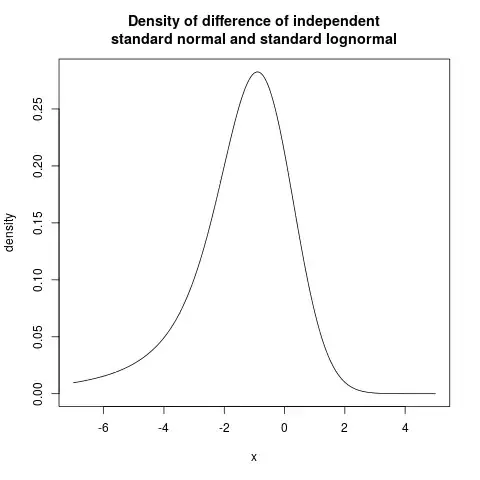
I have to study tolerance intervals for a distribution of a random variable Z that is given by the difference of a normal X minus a (independent) lognormal Y.

To begin with I tried to get an expression for the PDF of Z, but I got stuck in solving the integral

$f_Z(z)=\int_{-\infty}^\infty f_X(x)f_Y(x-z)dx$.

where $f_X$ is the PDF of a normal random variable and $f_Y$ is the PDF of a lognormal RV independent from X. I don't even know if this integral is solvable in terms of elementary functions.

Is there any document I could read to progress in my analysis towards a tolerance interval? Do you believe this kind of distribution is tractable in a theoretical way?

Note that $-Z$ will have the distribution of the convolution of a lognormal and a normal, so it's possible that Hawkins, D. (1991), "The convolution of the normal and lognormal distributions", *Suid-Afrikaanse Statistiese Tydskrif* (South African Statistical Journal) 25, 99–128. might have something of relevance to you, but unfortunately I can't look at it easily. However, I very strongly doubt that the convolution will be analytically tractable. — Glen_b, Mar 15 '16 at 09:25
You can try to adapt the solution here: https://stats.stackexchange.com/questions/152850/difference-of-two-i-i-d-lognormal-random-variables/176374#176374 — kjetil b halvorsen, Sep 22 '17 at 19:07

kjetil b halvorsen · Answer 1 · 2018-01-31T10:21:32.093

There is no reason to expect a simple solution in closed form, so we will go directly to a solution by numerical integration, following Difference of two i.i.d. lognormal random variables and PDF from difference of two Weibull distributions. We will only look at the case with a standard normal distribution, and a standard lognormal. Let $X$ be a standard normal random variate (with density $\phi$ and cdf $\Phi$) and $Y$ a standard lognormal variate (independent from $X$) with density $\phi(\ln y)/y$ and cdf $\Phi(\ln y)$. Then the density of the difference $D=X-Y$ is given by $$ f_D(t) = \int_0^\infty f_X(y+t) f_Y(y)\; dy $$ Then we define:

dDIFF <-  function(x) {
    res  <- x
    for (xx in seq(along=x)) {
        res[xx]  <-  integrate(function(y) dnorm(y+x[xx]) * dlnorm(y),  lower=0.0,  upper=+Inf)$value
    }
    return(res)
}

and show a plot of this density function:

For most uses such an numerical solution is very fast, and should be enough.

Difference between gaussian and lognormal

1 Answers1