suitable non-linear equation to capture a 'J-shaped' relationship between x and y

Question

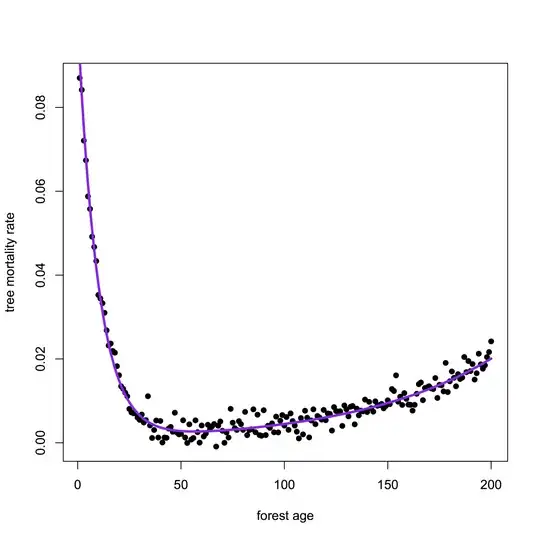
I am trying to model the relationship between forest age and individual tree mortality rate. The probability of mortality declines rapidly as forests go from being very young, and then creeps back up as they age (Juveniles more likely to die than intermediate aged trees. After this initial decline in mortality probability, mortality creeps back up as a function of age).

Here are some example data generated in R, and a plot of the relationship. I build the example data using two independently parameterized exponential functions, and then summing them together.

#age range, combine two curves to get J
age <- seq(1:200)
age.m1 <- 0.1    * exp(-age * .1) #mortality rate declines initially from juvenile stage
age.m2 <- 0.001 * exp(age* 0.015) #mortality rate creeps up as trees get older
age.m3 <- age.m1 + age.m2 #combine the two mortality rates
#generate some scatter in the data to plot
scatter <- age.m3 + rnorm(length(age.m3),0, 0.002)

#plot data and true relationship
plot(scatter, pch=16, ylab = 'tree mortality rate', xlab='forest age')
lines(smooth.spline(age.m3), lwd=3, col='purple')

The outcome looks like this:

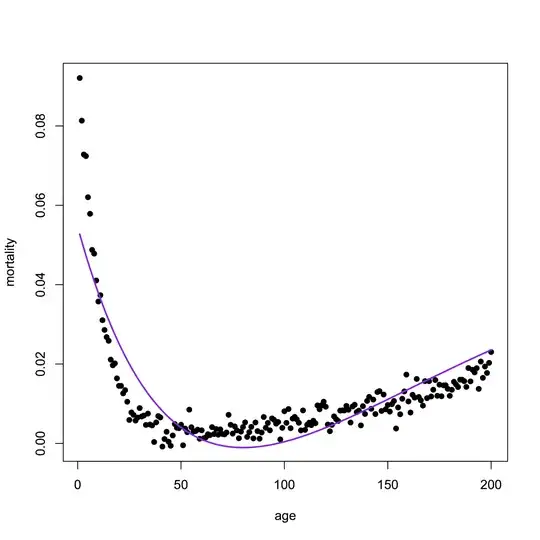
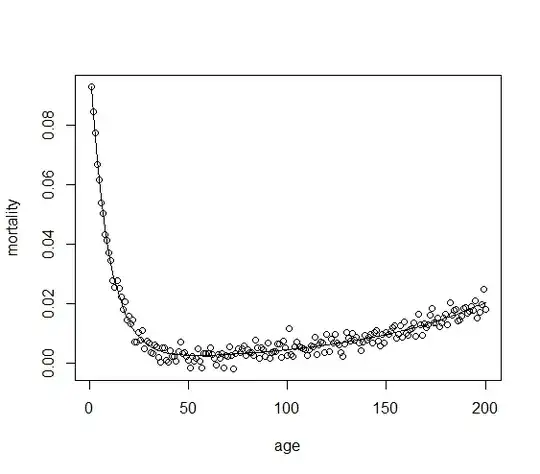
I'd like to fit a function that could capture this non-linear relationship, so that I could compare the parameters of these fits to different sets of data. Specifically, I'm asking:

1. Which equation could fit an asymmetric curve like this using any statistical software?
2. Can you demonstrate it works using the nls package, or similar, in R?

Answer 1

FIRST APPROACH:

Hurst et al. use the following form for a similar problem (as far as I can see):

mortality = a + b * age * exp(c * age)

where a, b, and c are parameters. The call to nls would be along the lines

dat <- data.frame(age=age, mortality=scatter)
fit <- nls(
    mortality ~ a + b * age * exp(c*age), 
    data=dat, start=list(a=0.05, b=-0.001, c=-0.001)
)
plot(mortality~age, data=dat)
lines(predict(fit))

where dat is the data.frame with your data, including the columns mortality and age. The fit does not look very nice, though.

SECOND APPROACH:

To exploit the known functional relation, you can use constrained optimisation to get a reasonable fit:

ll <- function(par, dat) -sum(dnorm(dat[,"mortality"], 
        mean=par[1]*exp(par[2]*dat[,"age"]) +   
             par[3]*exp(par[4]*dat[,"age"]), 
        sd=par[5], log=TRUE)
)

fit_mle <- constrOptim(
    theta=c(1,-0.05,1, 0.05, 1), 
    f=ll, grad=NULL, 
    ui=diag(c(1,-1,1,1,1)), ci=rep(0,5), dat=dat
)

p <- fit_mle[["par"]]
y <- p[1]*exp(p[2]*age)+p[3]*exp(p[4]*age)
plot(mortality~age, data=dat)
lines(y)

The important constraints are that the second parameter needs to be negative and the fourth parameter positive.

Answer 2

You just need to choose some sensible options in nls. Here I used constrained nls, forcing the coefficients to have opposite signs. I ran this after your code above:

mfit=nls(scatter ~ a1*exp(-b1*age)+a2*exp(b2*age),
    start=list(a1=.01,a2=.02,b1=.04,b2=.04),lower=list(0,0,0,0),
    algorithm="port",trace=TRUE)
 lines(age,fitted(mfit),col="yellow2",lwd=2,lty=3)

The fitted curve is the light dashed line right up the middle of the purple curve