0

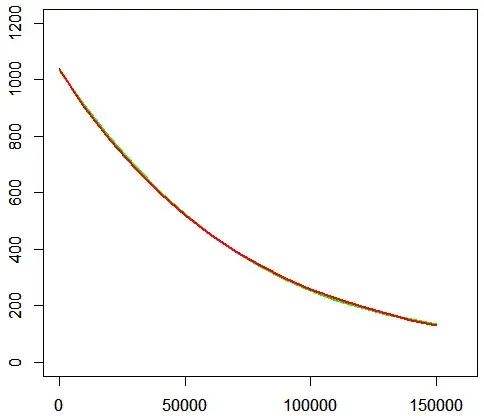
Following code was used to fit a function to my data;

# dataset
x <- c(0,10000,20000,30000,40000,50000,60000,70000,80000,90000,100000,110000,120000,130000,140000,150000)
y <- c(1034,908,794,693,602,523,452,392,339,294,255,221,195,171,152,135)

# visualize dataset
plot(x,y, xlim=c(0,160000), ylim=c(0,1200), pch=".")
lines(x, y,lwd=2, col="green")

# fit model
model <- lm(log(y)~x)
prediction <- exp(predict(model,list(Time=y)))

# visualize model
par(new=T)
plot(x,prediction, xlim=c(0,160000), ylim=c(0,1200), pch=".",xlab="", ylab="")
lines(x, prediction,lwd=2, col = "red", xlab = "Time (s)", ylab = "Counts")

Values created by predict() fit nice to my data;

plot

Following output is created by summary(model);

Call:
lm(formula = log(y) ~ x)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.024165 -0.011078 -0.002164  0.009068  0.036583 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.945e+00  7.542e-03   920.9   <2e-16 ***
x           -1.384e-05  8.567e-08  -161.6   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0158 on 14 degrees of freedom
Multiple R-squared:  0.9995,    Adjusted R-squared:  0.9994 
F-statistic: 2.61e+04 on 1 and 14 DF,  p-value: < 2.2e-16

As far I'm aware I'm fitting the following model; right?

$\log(y)=X\beta+\epsilon$;

I'm not able to formulate the equation based on above output...
Unfortunately the following (closely related) question did not help me.
How to translate the results from lm() to an equation?

How to formulate the equation? Any help is greatly appreciated! Thanks!

Community
  • 1
Anne
  • 101
  • 1
  • 2
    Could you be more specific about your problem? The thread you link to appears to address all the issues you mention. – whuber May 27 '16 at 18:32
  • Thanks for your quick response! Somehow I completely missed the obvious solution.... Added answer in case anyone might be as foolish as me `;)` – Anne May 27 '16 at 20:38

1 Answers1

0

How could I've missed the following... I'm sorry!

x <- c(0,10000,20000,30000,40000,50000,60000,70000,80000,90000,100000,110000,120000,130000,140000,150000)
y <- exp(6.945+x*-1.384e-05)

Output;

[1]   1037.9470  903.7927  786.9778  685.2611  596.6914  519.5692  452.4150  393.9405  343.0239
[10]  298.6881   260.0828  226.4672  197.1964  171.7088  149.5155  130.1907
Anne
  • 101
  • 1