1

I am trying to simulate random diffusion of particles using a random walk diffusion model. I have used probabilities of movement of particles in a 2D area, to be 1/4 in all 4 directions. The confusion that I am having is whether to assign the corner probabilities as still 1/4 in the available directions (picture 1) 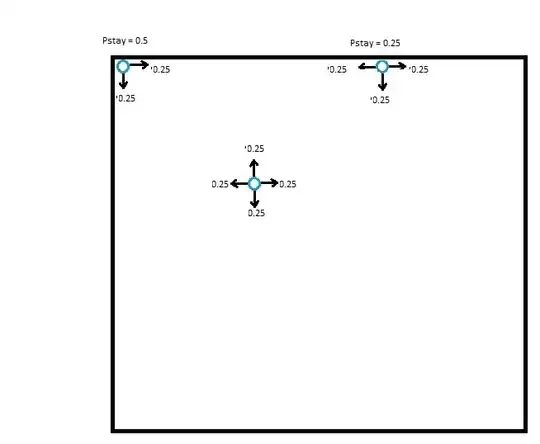enter image description hereor increase it, as the number of directions has decreased e.g. if 2 available directions then, 1/2 probability as shown in picture 2?

enter image description here

Rizwan Ali
  • 11
  • 1
  • 3
    Why do you have bounds (a bounding box)? What is the behavior of the underlying physical situation (diffusion of particles) when the particles are at or transition to a bound (or corner)? Reflecting, absorbing, other? – Mark L. Stone May 26 '16 at 17:06
  • 3
    not sure if this is a statistics question. In any case, the answer depends on what you want to have happen at the boundary (as @MarkL.Stone comments). Periodic boundary condition (walker disappears of the edge, reappears on the other side of the domain) is another possibility. – Ben Bolker May 26 '16 at 17:07
  • 2
    It is an axiom of probabilities that their total must always sum to 1. BTW (@Ben), code for the periodic random walk appears at http://mathematica.stackexchange.com/questions/13113 . – whuber May 26 '16 at 17:10
  • @MarkL.Stone: I am characterizing diffusion of water molecules in a glass. Thus I have finite bounds. The particles are bound to stay in this square region. But I am not sure whether I should model them as 1/4 probability in all 4 directions, even when they are at boundary, or not i.e. if they are on boundary, the particles would not know whether they are at boundary or not and thus try to move even in the direction of wall, which they could not, and hence, that probability would add to the probability of just staying at their place. – Rizwan Ali May 26 '16 at 19:53

0 Answers0