L2-regularized MLR using caret and how to make sure I am using the best tuned model

Question

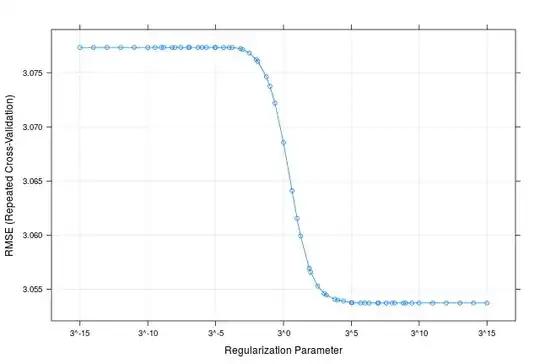
I am trying to do L2-regularized MLR on a data set using caret. Following is what I have done so far to achieve this:

r_squared <-  function ( pred, actual){
    mean_actual = mean (actual)
    ss_e = sum ((pred - actual )^2)
    ss_total = sum ((actual-mean_actual)^2 )
    r_squared = 1 - (ss_e/ss_total)
}

df = as.data.frame(matrix(rnorm(10000, 10, 3), 1000))
colnames(df)[1] = "response"
set.seed(753)
inTraining <- createDataPartition(df[["response"]], p = .75, list = FALSE)
training <- df[inTraining,]
testing  <- df[-inTraining,]
testing_response <- base::subset(testing,
                                 select = c(paste ("response")))
gridsearch_for_lambda =  data.frame (alpha = 0,
                                      lambda = c (2^c(-15:15), 3^c(-15:15)))
regression_formula = as.formula (paste ("response", "~ ", " .", sep = " "))
train_control = trainControl (method="cv", number =10,
                              savePredictions =TRUE , allowParallel = FALSE )
model = train (regression_formula,
                           data = training,
                           trControl = train_control,       
                           method = "glmnet",
                           tuneGrid =gridsearch_for_lambda,
                           preProcess = NULL
            )
prediction = predict (model, newdata = testing)
testing_response[["predicted"]] = prediction
r_sq = round (r_squared(testing_response[["predicted"]],
              testing_response[["response"]] ),3)

Here I am concerned about assurance that the model I am using for prediction is the best one (the optimal tuned lambda value).

P.S.: The data is sampled from random normal distribution, which is not giving a good R^2 value, but I want to get the idea correctly

Answer 1

If I understand correctly, this leaves you with two tasks: model tuning and subsequent model selection (you should possibly consider multiple model types when choosing the best suited model for a particular task).

For model tuning you could use a hyperparameter grid search, as you already did in the code above. If you get good results for certain ranges of parameters, it would be reasonable to employ a more fine grained parameter grid in those regions. You can approximate the "optimal" parameter configuration iteratively this way, but beware of possible over-optimizing and a resulting overfitting. BTW: more sophisticated approaches than parameter grid searches exist (e.g. genetic algorithms) - you could employ such in case your real data represents a more sophisticated problem where parameter search is quite difficult.

As model selection can overfit as well, it is a good idea to evaluate it the same way and time as hyperparameter tuning. A reasonable choice would be to evaluate all desired model types and model hyperparameters using repeated cross validation, then chose an optimal model from the repeatedcv performances, and subsequently compute its real performance on a held-back and yet unseen test data set.

# this snipped relies on the snipped in the question!

train_model <- function(method, tuneGrid=NULL, ...) {
  model <- train(form = regression_formula,
                 data = training,
                 trControl = trainControl (method = "repeatedcv", 
                                           number = 10, 
                                           repeats = 10, 
                                           savePredictions = T, 
                                           allowParallel = F, 
                                           returnResamp = 'final'),
                 ...,
                 method = method,
                 tuneGrid = tuneGrid)
  model
}

# train different models
models <- list()
models$glm <- train_model(method = 'glm', model=F)
models$glmnet <- train_model(method = 'glmnet', tuneGrid=gridsearch_for_lambda)
models$svmLinear <- train_model(method = 'svmLinear', tuneGrid=expand.grid(C=3**(-5:5)))

For models with hyperparameters, caret has a built in plotting function to visualize performance over hyperparameter sets. This is where you can see which parts of the grid performed well so far, and which parts you could possible make more fine grained:

plot(models$svmLinear, scales=list(x=list(log=3)))
plot(models$glmnet, scales=list(x=list(log=3)))

Using caret::resamples different models can be compared to each other. This is what could be used to decide upon which model performed best on your task:

resample <- resamples(models)
summary(resample)
bwplot(resample)