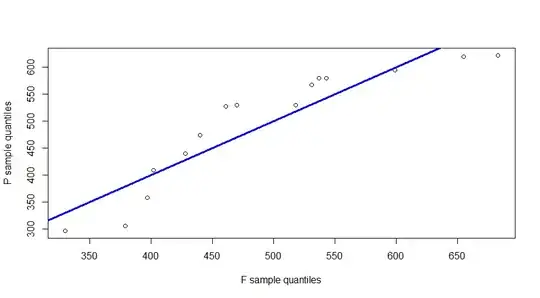
I'm a bit confused with interpretation of Sample Sample Q-Q plot produced by qqplot R function.
OUT_number_F=c(440, 461, 379, 518, 402, 470, 599, 543, 330, 537, 683, 397, 428, 531, 655)
OUT_number_P=c(530, 409, 296, 474, 305, 567, 580, 579, 358, 594, 530, 440, 619, 622, 527)
qqplot(OUT_number_F,OUT_number_P,xlab = "F sample quantiles",ylab = "P sample quantiles")
abline(0,1,col="blue",lwd=3)
So, based on the image above, i could make the follows conclusion: a) The samples came from the two completely different distributions (only just for instance, let's say, normal and poisson's distributions) b) The samples could came from the same distribution (e.g. normal), but be skwed relatively each other (as i understand, data in this case came from two different normal distributions)
Which statements above are correct? The second question. In the code example to add blue line to the Q-Q plot i used command :
abline(0,1,col="blue",lwd=3)
As i know there is not any special Rfunction for that (i can not apply qqline() function in this case). Is my approach the most accurate and correct way to add line to the Sample Sample Q-Q plot?