I have data on weight of a group of people after and before a diet. I want to see if weight loss is distributed normally.
> weightloss <- dietA$Peso.inicial-dietA$Peso.final
[1] 7.48 3.71 4.30 5.47 3.80 6.31 7.76 4.07 3.70 4.11 4.96 4.63 5.18 5.68 4.76 1.87
[17] 7.80 3.29 7.23 6.67 3.96 0.72 4.36 0.10 2.30 7.15 5.61 7.20 5.27 7.86 4.81 6.08
[33] 5.90 5.16 1.60 5.50 6.16 5.99 6.36 0.91
I ran the Shapiro-Wilk test using R:
> shapiro.test(weightloss)
Shapiro-Wilk normality test
data: weightloss
W = 0.95123, p-value = 0.08357
Now, if I assume the significance level at 0.05 then the p-value is larger than alpha (0.08357> 0.05) and I cannot reject the null hypothesis about the normal distribution, so can we accept the null hypothesis? I know that divergent views exist on this (see Interpretation of Shapiro-Wilk test, What is Hypothesis Testing? and When to use Fisher and Neyman-Pearson framework?), in addition the difference between values is short and with significance level at 0.1 we can reject the null hypothesis.
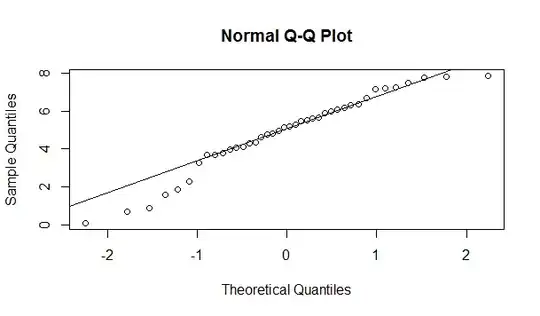
I try to see other way that gave me other element like QQPlot:
> qqnorm(weightloss)
> qqline(weightloss)
As you can see the first points are rightmost and at the end we have one point rightmost too, so maybe I can conclude not normality of the data(see How to interpret a QQ plot). In order to see other points I create a histogram
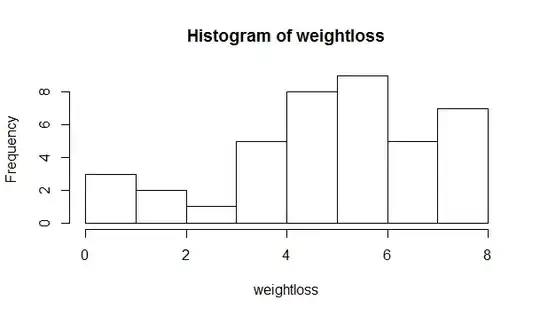
So with this almost I can say that the sample hasn't a normal distribution or I can accept normality with uncertainty. I am not sure about this.