I have a very strange behavior where I am trying to run PCA on the MNIST data set and then I check the test and train error. However, it seems that I get that the test error is lower than my train error, which seems totally bizarre for me. Is this normal? Has people ever experienced this type of behavior on the MNIST data set?
To make my bug totally reproducible I will give a link to my github code (i.e. the exact data set I used is there, and its small). Also, the code I ran is super simple:
clear;clc;
load('data_MNIST_original_minist_60k_10k_split_train_test');
[N_train, D] = size(X_train) % (N_train x D)
[N_test, D] = size(X_test) % (N_test x D)
%% preparing model
K = 10;
[coeff, ~, ~, ~, ~, mu] = pca(X_train); % (D x R) = Rows of X_train correspond to observations and columns to variables.
%% Learn PCA
X_train = X_train'; % (D x N) = (N_train x D)'
X_test = X_test'; % (D x N) = (N_test x D)'
U = coeff(:,1:K); % (D x K) = K pca's of dimension D
X_tilde_train = (U * U' * X_train); % (D x N_train)= (D x N)' = ( (D x K) x (K x D) x (D x N) )'
X_tilde_test = (U * U' * X_test); % (D x N_test)= (D x N)' = ( (D x K) x (K x D) x (D x N) )'
train_error_PCA = (1/N_train)*norm( X_tilde_train - X_train ,'fro')^2
test_error_PCA = (1/N_test)*norm( X_tilde_test - X_test ,'fro')^2
then I got:
train_error_PCA =
29.0759
test_error_PCA =
28.8981
is this normal?
is this why people add background noise to the MNIST data set?
I am just using standard PCA library so I can't possibly see what might have gone wrong
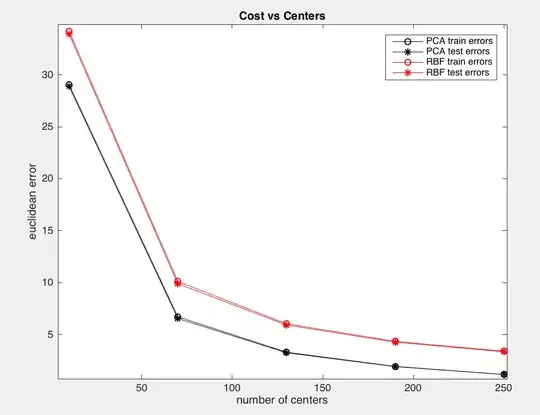
I have also tested this with different non-linear auto-encoders, for example, I tried a 1 layer Radial Basis Function (RBF) and it produces the same strange result:
if you get close enough, the little circle (train) is above each start (test). Which is not expected.
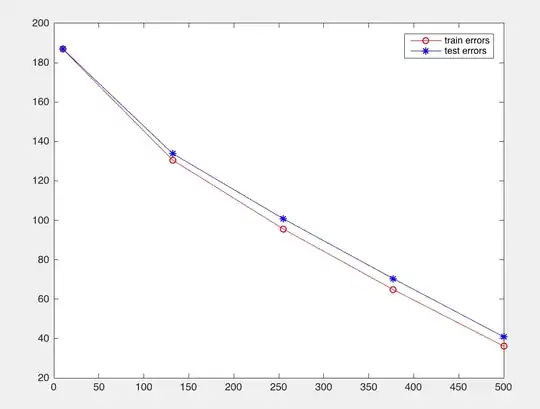
I have now made the same test but with a more complicated MNIST data set that can be found (https://sites.google.com/a/lisa.iro.umontreal.ca/public_static_twiki/variations-on-the-mnist-digits) and I also included it with the git large file tracking (https://git-lfs.github.com/) on the repo (it will eventually reach github). Now with this it seems the train error is lower than test, as I assume it should be:
and ran the code:
clear;clc;
%load('data_MNIST_original_minist_60k_10k_split_train_test');
load('mnist_background_random_test');
load('mnist_background_random_train');
X_train = mnist_background_random_train(:,1:784);
X_test = mnist_background_random_test(:,1:784);
[N_train, D] = size(X_train) % (N_train x D)
[N_test, D] = size(X_test) % (N_test x D)
%%
[coeff, ~, ~, ~, ~, mu] = pca(X_train); % (D x R) = Rows of X_train correspond to observations and columns to variables.
num_centers = 5; % <-- change
start_centers = 10;
end_centers = 500;
centers = floor(linspace(start_centers, end_centers, num_centers));
train_errors = zeros(1,num_centers);
test_errors = zeros(1,num_centers);
for i=1:num_centers
K = centers(i);
%% preparing model
U = coeff(:,1:K); % (D x K) = K pca's of dimension D
X_train_T = X_train'; % (D x N) = (N_train x D)'
X_test_T = X_test'; % (D x N) = (N_test x D)'
X_tilde_train = (U * U' * X_train_T); % (D x N_train)= (D x N)' = ( (D x K) x (K x D) x (D x N) )'
X_tilde_test = (U * U' * X_test_T); % (D x N_test)= (D x N)' = ( (D x K) x (K x D) x (D x N) )'
train_error_PCA = (1/N_train)*norm( X_tilde_train - X_train_T ,'fro')^2;
test_error_PCA = (1/N_test)*norm( X_tilde_test - X_test_T ,'fro')^2;
train_errors(i) = train_error_PCA;
test_errors(i) = test_error_PCA;
end
fig = figure;
plot(centers, train_errors, '-ro', centers, test_errors, '-b*');
legend('train errors', 'test errors');
I will leave the question because I am not sure if I truly fixed the error or not.