I have a statistical question.
I have data from an experiment with two conditions (dichotomous IV: 'condition'). I also want to make use of another IV which is metric ('hh'). My DV is also metric ('attention.hh'). I've already run a multiple regression model with an interaction of my IVs. Therefore, I centered the metric IV by doing this:
hh.cen <- as.numeric(scale(data$hh, scale = FALSE))
with these variables I ran the following analysis:
model.hh <- lm(attention.hh ~ hh.cen * condition, data = data)
summary(model.hh)
The results are as follows:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.04309 3.83335 0.011 0.991
hh.cen 4.97842 7.80610 0.638 0.525
condition 4.70662 5.63801 0.835 0.406
hh.cen:condition -13.83022 11.06636 -1.250 0.215
However, the theory behind my analysis tells me, that I should expect a quadratic relation of my metric IV (hh) and the DV (but only in one condition).
Looking at the plot, one could at least imply this relation:
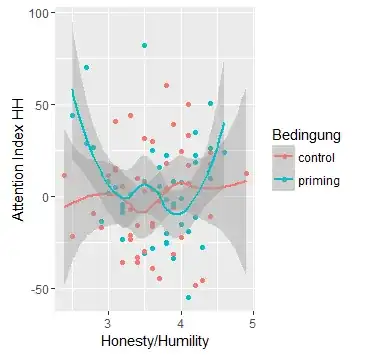
Of course I want to test this statistically. However, I'm struggling now if and when to center the metric IV, because the interaction is still important (as there is only a quadratic relation in one condition).
Do I first center the variable and then compute the quadratic term or the other way round? Do I compute the interaction with both the linear and the quadratic term or only one of them?
My gut feeling would suggest something like this:
hh.sqr <- hh * hh
sqr.model.hh <- lm(attention.hh ~ hh.sqr + hh.cen * condition, data = data)
summary(sqr.model.hh)
In a nutshell, I want to test whether there is a quadratic relation in one of my conditions. However, I am not sure which terms I have to include into the model (or whether I calculate hh.sqr * condition vs. hh.cen * condition -- or both)?!