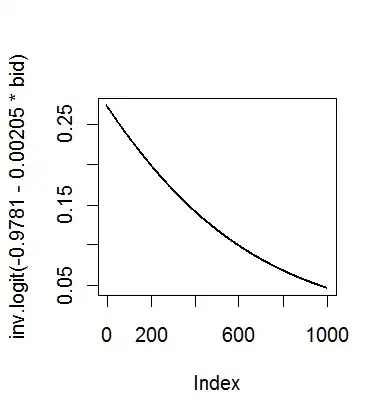
Let's say that I generate the probability of an outcome based on a certain factor and plot the curve of that outcome. Is there any way to extract the equation for that curve from R?
> mod = glm(winner~our_bid, data=mydat, family=binomial(link="logit"))
> summary(mod)
Call:
glm(formula = winner ~ our_bid, family = binomial(link = "logit"),
data = mydat)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.7443 -0.6083 -0.5329 -0.4702 2.3518
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -9.781e-01 2.836e-02 -34.49 <2e-16 ***
our_bid -2.050e-03 7.576e-05 -27.07 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 42850 on 49971 degrees of freedom
Residual deviance: 42094 on 49970 degrees of freedom
AIC: 42098
Number of Fisher Scoring iterations: 4
> all.x <- expand.grid(winner=unique(winner), our_bid=unique(our_bid))
> all.x
> won = subset(all.x, winner == 1)
> y.hat.new <- predict(mod, newdata=won, type="response")
> options(max.print=5000000)
> y.hat.new
> plot(our_bid<-000:1000, predict(mod, newdata=data.frame(our_bid<-c(000:1000)),
type="response"))
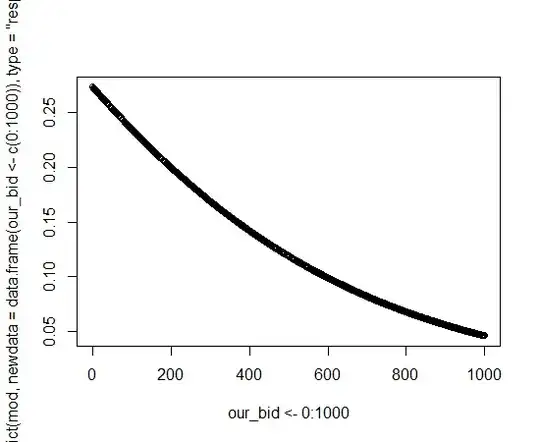
How can I go from this probability curve to an equation in R? I was hoping for something like:
Probability = -0.08*bid3 + 0.0364*bid2 - 0.0281*bid + 4E-14