2

So based from this link

http://www.simafore.com/blog/bid/107702/2-ways-of-using-Naive-Bayes-classification-for-numeric-attributes

I began to realize it might be a good idea to compute the pdf of each of my features vs. class to be properly compute my posterior probabilities..

My dataset consist of 4000 observations which each have 324 features. The 4000 observations are divided into ten classes.

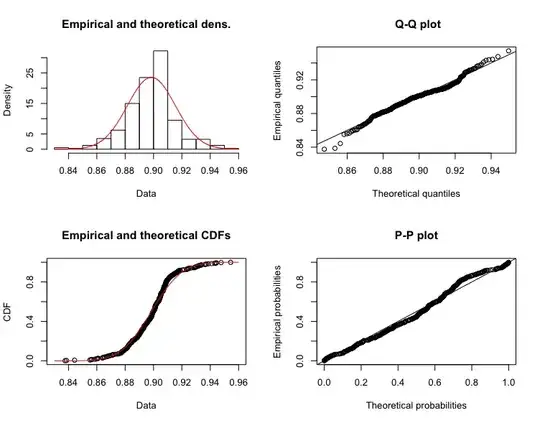
I first tried to fit my dataset to a QQ-plot, which clearly showed that my dataset seems normally distributed.

enter image description here

Then I tried this cullen and frey graph, which kinda provided me with an different answer...

enter image description here

I am not sure whether i am interpreting the second graph incorrectly?, but is it indicating that feature1 of class 1 is distributed logisticly or am i reading it incorrectly?

Update

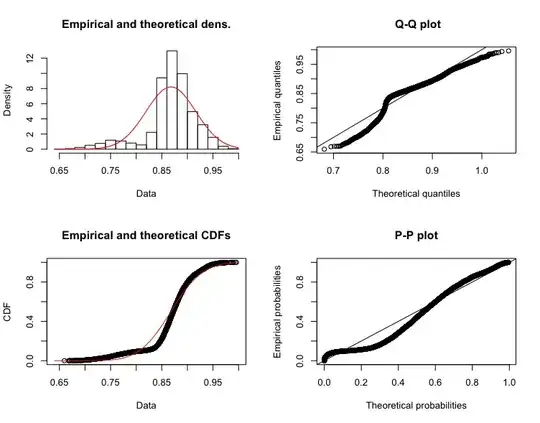
I tried creating the same plot as in first one for a larger sample size (80000) which as @Tim mentions shapiro.wilks test won't work. But interestingly is the QQ-plot also beginning to deviate from normality..

enter image description here

Why am I interested? I want extract the most accurate and highest score as possible, but if the model I think it comes from is not accurate, then I might have to change the model, and compute my probabilities another way, but how would it affect Naive bayes, that the distribution of the dataset is not normal?

Bob Burt
  • 545
  • 1
  • 6
  • 23
  • Try a Wilks-Shapiro test for normality? – Jabernet Apr 18 '16 at 20:42
  • 1
    output : W = 0.97812, p-value = 9.657e-06 – Bob Burt Apr 18 '16 at 20:43
  • 1
    No real life data is exactly normally distributed. Why are you interested in normality? See https://stats.stackexchange.com/questions/2492/is-normality-testing-essentially-useless – Tim Apr 18 '16 at 20:46
  • 1
    That's a small number, for sure. I suggest you make your own decision but a standard alpha to reject region is less that .05 (90% 2 sided test for normality) so I think it's clear that the data is not normal. – Jabernet Apr 18 '16 at 20:47
  • I suggest that you try to look at the issue in a non-dichotomous manner. Data are almost never truly normally distributed, at least because the normal distribution extends infinitely in both directions. (Are negative values possible in your data?) You should be asking if your data are normal enough for analytical purposes. Looking at the Q-Q plot, I would say that they are normal enough for my purposes. The discrepancy is tiny. – Michael Lew Apr 18 '16 at 21:12
  • 2
    @Jabernet with sample size of 40000 normality test will reject the null for nearly *any* data (e.g. https://stats.stackexchange.com/questions/12225/methods-to-check-if-my-data-fits-a-distribution-function), in R `shapiro.test` even returns error `sample size must be between 3 and 5000` for sample sizes over 5000... – Tim Apr 18 '16 at 21:14
  • @Tim My mistake... 4000 data points not 40000 – Bob Burt Apr 18 '16 at 21:15
  • @BobBurt - Visual inspection of QQ plot says there is a flat region (gaussian) and a non-flat region (exponential?). It also has an intercept that is non-zero. Given those, it might be decently well fit by a 2-component mixture model where one of the components is a constant offset exponential-like distribution. – EngrStudent May 22 '17 at 23:57

0 Answers0