20

Are reduced rank regression and principal component regression just special cases of partial least squares?

This tutorial (Page 6, "Comparison of Objectives") states that when we do partial least squares without projecting X or Y (i.e., "not partial"), it becomes reduced rank regression or principal component regression, correspondingly.

A similar statement is made on this SAS documentation page, Sections "Reduced Rank Regression" and "Relationships between Methods".

A more fundamental followup question is whether they have similar underlying probabilistic models.

Community
  • 1
Minkov
  • 415
  • 3
  • 7

1 Answers1

20

These are three different methods, and none of them can be seen as a special case of another.

Formally, if $\mathbf X$ and $\mathbf Y$ are centered predictor ($n \times p$) and response ($n\times q$) datasets and if we look for the first pair of axes, $\mathbf w \in \mathbb R^p$ for $\mathbf X$ and $\mathbf v \in \mathbb R^q$ for $\mathbf Y$, then these methods maximize the following quantities:

\begin{align} \mathrm{PCA:}&\quad \operatorname{Var}(\mathbf{Xw}) \\ \mathrm{RRR:}&\quad \phantom{\operatorname{Var}(\mathbf {Xw})\cdot{}}\operatorname{Corr}^2(\mathbf{Xw},\mathbf {Yv})\cdot\operatorname{Var}(\mathbf{Yv}) \\ \mathrm{PLS:}&\quad \operatorname{Var}(\mathbf{Xw})\cdot\operatorname{Corr}^2(\mathbf{Xw},\mathbf {Yv})\cdot\operatorname{Var}(\mathbf {Yv}) = \operatorname{Cov}^2(\mathbf{Xw},\mathbf {Yv})\\ \mathrm{CCA:}&\quad \phantom{\operatorname{Var}(\mathbf {Xw})\cdot {}}\operatorname{Corr}^2(\mathbf {Xw},\mathbf {Yv}) \end{align}

(I added canonical correlation analysis (CCA) to this list.)

I suspect that the confusion might be because in SAS all three methods seem to be implemented via the same function PROC PLS with different parameters. So it might seem that all three methods are special cases of PLS because that's how the SAS function is named. This is, however, just an unfortunate naming. In reality, PLS, RRR, and PCR are three different methods that just happen to be implemented in SAS in one function that for some reason is called PLS.

Both tutorials that you linked to are actually very clear about that. Page 6 of the presentation tutorial states objectives of all three methods and does not say PLS "becomes" RRR or PCR, contrary to what you claimed in your question. Similarly, the SAS documentation explains that three methods are different, giving formulas and intuition:

[P]rincipal components regression selects factors that explain as much predictor variation as possible, reduced rank regression selects factors that explain as much response variation as possible, and partial least squares balances the two objectives, seeking for factors that explain both response and predictor variation.

There is even a figure in the SAS documentation showing a nice toy example where three methods give different solutions. In this toy example there are two predictors $x_1$ and $x_2$ and one response variable $y$. The direction in $X$ that is most correlated with $y$ happens to be orthogonal to the direction of maximal variance in $X$. Hence PC1 is orthogonal to the first RRR axis, and PLS axis is somewhere in between.

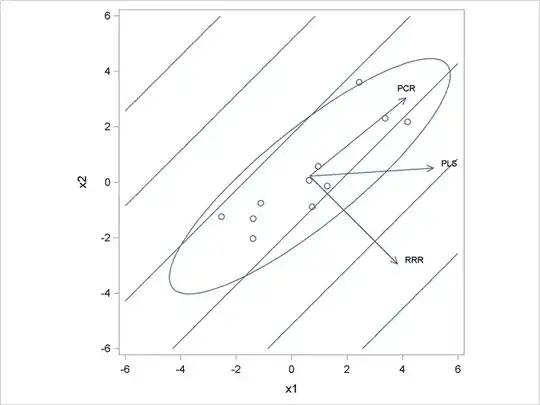
PCR, PLS, RRR

One can add a ridge penalty to the RRR lost function obtaining ridge reduced-rank regression, or RRRR. This will pull the regression axis towards the PC1 direction, somewhat similar to what PLS is doing. However, the cost function for RRRR cannot be written in a PLS form, so they remain different.

Note that when there is only one predictor variable $y$, CCA = RRR = usual regression.

amoeba
  • 93,463
  • 28
  • 275
  • 317
  • 6
    The table at the end is very helpful. Based on that table, one might consider PCA, RRR, and CCA to be "special cases" of PLS if you also think that bicycles and unicycles are special cases of a tricycle. I don't tend to think that way. – EdM Apr 12 '16 at 15:19
  • 2
    @EdM, I think one can say that all these methods are special cases of some unifying method that does not really have a name (but one can invent it!). But the name "PLS" already has an established meaning and this meaning does not include any of these other techniques. – amoeba Apr 12 '16 at 15:25
  • 1
    And thanks! I decided now to move the table to the beginning of the answer :) – amoeba Apr 12 '16 at 15:28
  • @amoeba. Thanks a lot for the answer! As you can see, when $X$ is $N(0, I)$ in PLS, it becomes RR. This is what I am thinking as a "special case". I totally agree with you, there should be a unifying method that is not exactly named PLS. So do you know how to formulate this unifying method? – Minkov Apr 12 '16 at 23:05
  • 3
    @Moskowitz: Yes, if $X$ is whitened then PLS=RRR and if $Y$ is whitened then RRR=CCA; if both are whitened then PLS=RRR=CCA. However, PCR remains different. Regarding the unifying method, well, one can just say that we maximize $\mathrm{Var}(Xw)^\alpha\cdot \mathrm{Corr}(Xw,Yv)^\beta\cdot \mathrm{Var}(Yv)^\gamma$ and get various methods for various values of alpha, beta, and gamma. Don't think it's very useful though. – amoeba Apr 12 '16 at 23:17
  • @amoeba. If we view this problem from a generative model perspective, we can think about $(X,Y)\sim N(0,\Sigma)$, where $\Sigma$ is a covariance matrix with four blocks. Then the question is, for what configurations of $\Sigma$, the solutions to RRR, PLS, and CCA are the maximum likelihood estimators for this generative model? – Minkov Apr 12 '16 at 23:18
  • @Moskowitz: I think I see where you are going with this last question, but as currently formulated it does not make sense: ML estimators *of what*? You probably want to put latent variables in there and some mapping from them to $X$ and $Y$ (similarly to PPCA/FA models). If properly formulated, it might be an interesting question, but I think a new one. – amoeba Apr 12 '16 at 23:22
  • 1
    @Moskowitz: In general, when people talk about method A being a "special case" of method B, they mean that B is more general and A is equivalent to B with some specific parameters. They do *not* mean that A gives the same results as B under some special conditions on the dataset. Hence my answer to your question. – amoeba Apr 12 '16 at 23:24
  • @amoeba. Thanks for the comments. I meant that $\Sigma$ depends on the latent variables $w, v$, like in the PPCA model, as you have pointed out. I searched around, there seems to be very few paper talking about probabilistic CCA/PLS/RRR. – Minkov Apr 12 '16 at 23:30
  • @Moskowitz: In PPCA, $x\sim \mathcal N(Wz+\mu, \sigma^2 I)$, so the dependence of $x$ on $z$ is definitely not through the covariance matrix. In any case, there is something called "probabilistic CCA" (PCCA), it's pretty well established. But I don't think there are any probabilistic versions of PLS or RRR. – amoeba Apr 12 '16 at 23:34
  • The (not quite standard) PPCA model I am thinking is $x = wz + \mu \in R^p$, where $z \sim N(0,1)$, $w\in R^p$ and $\mu \sim N(0,I_p)$. Then the covariance of $x$ is $ww^T + I_p$. The goal is to estimate $w$. This is know as the spiked covariance model, which is frequently used in the PCA literature. – Minkov Apr 12 '16 at 23:40
  • @Moskowitz Ah, yes, okay. That's the same thing. Now I see what you meant. In any case, the comments here are not for extended discussions. Do you think your original question is resolved? – amoeba Apr 12 '16 at 23:44
  • @amoeba. Yes the original question is resolved. Thanks a lot! I really appreciate your help : ) I will open another thread to see if any one has interesting thoughts on that. Hopefully this can help others who encounter the same question. – Minkov Apr 12 '16 at 23:48
  • @amoeba. I have formulated the new question [here](http://stats.stackexchange.com/questions/206997/probabilistic-model-for-partial-least-squares-reduced-rank-regression-and-cano). Thanks again for your help. – Minkov Apr 13 '16 at 00:17
  • Based on this nice discussion I conclude that only PCA should be called dimensionality reduction because the only kind of dimension reduction that does not need to be accounted for when estimating overfitting comes from methods that consider only the $X$ space. – Frank Harrell Apr 13 '16 at 12:24
  • 1
    @Frank That's correct; I think it's okay to call all of them "dimensionality reduction" as long as one understands what that means. The crucial point you are making is that only PCA is *unsupervised* in the sense that it is done not considering $Y$. All other methods can certainly be subject to overfitting (I encounter that all the time) and need to be regularized, similar to any other regression-like model. – amoeba Apr 13 '16 at 14:06
  • missing PCR in the list (of what is the maximized/minimized quantity), can you please add it? – Tomas Dec 06 '19 at 10:20
  • @Curious No. PCR is the same as PCA in this context. PCR is PCA followed by standard regression. – amoeba Dec 06 '19 at 10:28
  • @amoebasaysReinstateMonica so PCR is first to do PCA and then do the regression on the principal axes? – Tomas Dec 06 '19 at 12:40
  • Yes exactly. @Curious. – amoeba Dec 06 '19 at 13:21
  • @user257566 No. RRR does not care about the variance in the X space. var(Xw) could be microscropic without affecting the RRR loss. – amoeba Dec 09 '19 at 09:32