8

I am using linear regression to estimate values that in reality are always non-negative. The predictor variables are also non-negative. For instance, regressing the number of years of education and age to predict salary. All variables in this case are always non-negative.

Due to the negative intercept, my model (determined with OLS) results in some negative predictions (when the value of the predictor variable is low with respect to the range of all values).

This topic has already been covered here, and I am also aware that forcing the intercept at 0 is discouraged, so it seems that I have to accept this model as the one I have to use. However, my question here is about the accepted norms and rules when evaluating such model. Are there any particular rules here? Specifically:

  • If I get a negative estimate can I just round it to 0?
  • If the observed value is 100, and the predicted value is -300, and I know that the minimum possible value is 0, is the error 400 or 100? For instance, when calculating the ME and RMSE.

If it is relevant to the discussion: I have used both simple linear regression and multiple linear regression. Both result in several negative values.

Edit:

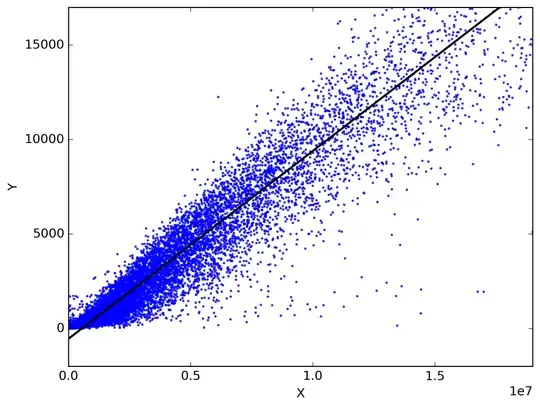
Here is the example of the samples with the fit:

Linear fit

The coefficients of the linear regression are 0.0010(x) and -540 (intercept).

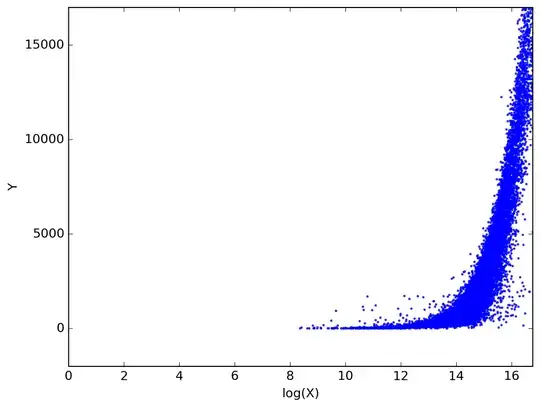
Here is what happens when I use log for the X:

Log

Is linear regression suitable here?

Community
  • 1
Mon
  • 81
  • 1
  • 1
  • 5
  • 3
    Your model is misspecified; you need a different kind of model. If your data cannot go below 0, and your model can, your model does not reflect the reality of your data. The difference may not be a big enough deal to worry about in some context, but it sounds like that isn't the case here. – gung - Reinstate Monica Mar 26 '16 at 21:26
  • @gung, I have updated the question with plots. – Mon Mar 28 '16 at 15:36
  • What are X & Y? Why can't Y be <0? – gung - Reinstate Monica Mar 28 '16 at 15:38
  • 1
    @gung, I'd like to avoid to go into too much detail since I don't find it relevant, so let's say that both X and Y are variables like income, age, rainfall, etc. which cannot be negative. – Mon Mar 28 '16 at 15:45
  • 2
    The details are definitely relevant to what kind of data X & Y are, & what kinds of relationships between them are possible. There is a very real limit to what we can advise you w/o more information. – gung - Reinstate Monica Mar 28 '16 at 16:03
  • 1
    If you are going to transform anything, it should be Y not X. Also, transforming X will not address your problem directly in any case. But check out Poisson regression, e.g. http://blog.stata.com/tag/poisson-regression/ – Nick Cox Mar 28 '16 at 18:00
  • Please give the confidence intervals (CI) of slope and intercept. If the CI of intercept includes zero, there is no problem setting it to be so. One problem is that the data is clearly bi-variate, so that ordinary least squares is biased (OLS). It may be necessary to use Theil or Passing-Bablok regression on this data. As a first step please take the logarithm of y and the logarithm of x, and look at the OLS residuals and 95% confidence intervals (CI). Taking the logarithms assumes non-negativity and proportional variability, which on visual inspection would be my first guess. – Carl Jun 22 '16 at 23:29

1 Answers1

5

You haven't given context, but you have linked to a post that offers one solution. I will assume that that solution is not applicable here.

Then another solution is to not use linear regression (simple or multiple) since they do not solve the problem you have.

First, though, let's use your of income as a function of age and education. Here, negative predicted values are reasonable because you are probably not interested in the income of newborn babies. However, there, taking log(income) is also reasonable, unless some people in your data set have no income.

But suppose that's not it. Then you can use a regression method that respects bounds on the dependent variable. One such is beta regression, which requires a DV that is between 0 and 1 - so you could scale your DV to be between 0 and 1 and then use beta regression.

But I would really urge you to add your actual variables to the question.

Peter Flom
  • 94,055
  • 35
  • 143
  • 276
  • Thanks for your answer. I have updated the question with plots that might be useful. – Mon Mar 28 '16 at 15:36
  • You haven't given context, you haven't said what X and Y are, you haven't said why Y cannot go below 0 and so, there is no way for anyone to help you. However, the solutions you propose in your question are all bad ones. – Peter Flom Mar 29 '16 at 11:07