0

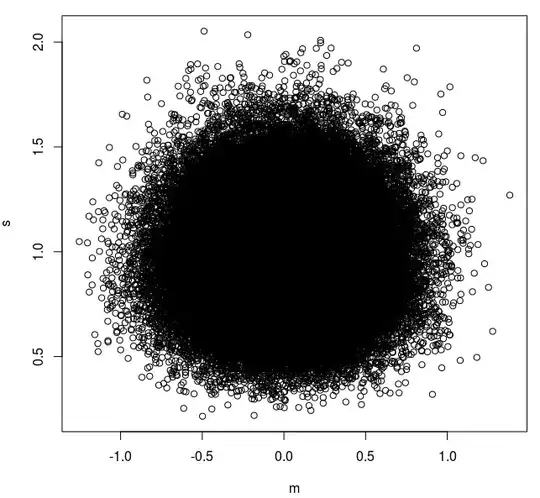
After correcting for a bug in my code in a previous question, I could simulate efficiently thousands of samples from the normal distribution N(0,1). I calculated the mean and standard deviation of each sample :

N <- 100000
n <- 10
d <- matrix(rnorm(N*n), nrow=10)
m <- colMeans(d)
s <- apply(d, 2, sd)

and plotted the standard deviation against the mean in a graph :

plot(s~m)

s~m | rnorm(10,0,1)

When generating another similar sample, is it possible to use its location in (s,m) 2D-space to determine whether, by reasonable evidence, it originates from a population distributed as N(0,1) ?

Actually, sample's SD is not normally distributed so one could use the space that encompasses 95% of all points as a limit within which a sample would be considered coming from the same population, and outside of which that sample would be considered as coming from another population with different population's mean and/or SD.

Is that reasoning related to p-values (as i suspect) ? Is it simply correct or not ? And is there a name for it ? Because it seems quite natural to me to think that a realized sample too far away from a given distribution (the null hypothesis, actually) , by mean AND standard deviation, could be considered different.

Community
  • 1
Rodolphe
  • 861
  • 5
  • 16
  • Broadly speaking the graph is what you expect from repeated sampling from _any_ distribution with mean 0 and SD 1. There would be small differences in the configuration depending on parent but just looking at the graph won't help you see them. More and more samples won't help given overplotting. The fallacy can be seen from a simple case. My mean is near 0 and my SD is near 1: does that show that I have N(0,1)? well, it is consistent with that idea, but also consistent with many other ideas. Consider also central limit theorems, so you can't infer a normal parent from this kind of evidence. – Nick Cox Mar 19 '16 at 09:32
  • As far as I understand, a classic parametric one sample t-test would need as null hypothesis that the sample is from a population following N(mu, theta). Then how can we test this hypothesis if the results will be consistent with any parent distribution with mean mu and standard deviation theta ? Does your argument also invalidates t-tests or am I misunderstanding something ? – Rodolphe Mar 19 '16 at 09:53
  • That's a completely different question. Your first question is close to what can one infer from the mean and SD about the shape of a distribution and the answer is nothing, with nothing else said. You're now asking something else. – Nick Cox Mar 19 '16 at 10:50
  • I think my question here has been misunderstood. I will try to rephrase it because most probably I did not explain it well enough and/or it was unclear. – Rodolphe Mar 19 '16 at 12:50

0 Answers0