Choosing options for fitting a regression model

Question

I am challenged by a simple, but hopefully interesting, data set.

Data

The data are driving times of ambulances to the scene (data$actual) as well as the driving times I created by using a GIS to calculate the time (data$simulation). The times differ because the GIS does not take into account that the ambulance drives faster than a standard car. Both times are in seconds. The actual data was provided in minutes, thus the steps in the data. You will find the data a the end of this post.

Goals

In order to use the GIS to predict which area the ambulance is able to cover I like to create a model that predicts a simulation driving time based on the actual time which I will then feed into the GIS simulation. This is necessary since the GIS itself does not account for the fact that ambulances drive faster than standard cars. The goal then is to use a longer driving time for the simulation in order to take this fact into account.

Approach

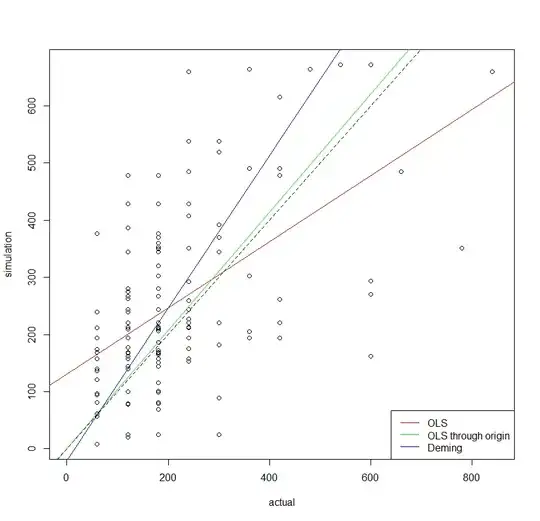
My first approach was to build a simple linear regression model for the data:

model1 <- lm(simulation ~ actual, data)

This gives site a bad R2 and residual standard error. In addition, I took into account the fact that if there is 0 seconds of actual driving time, there should also be 0 seconds of simulation driving time, resulting in:

model2 <- lm(simulation ~ 0 + actual, data)

Now the R2 drastically increases but the residual standard error also increases. Another thought involves the fact that the ambulance should always be faster than the normal car. So I filtered the data for simulation > actual and created a third model:

newData <- data[data$simulation > data$actual,]
model3 <- lm(simulation ~ 0 + actual, newData)

This again increases the R2 and now also reduces the error even below the value of model1.

My question

Is this a legitimate way to handle the data given what I try to create? I think reducing the amount of data will often yield better results since less data points need to be taken care of. In addition, if you look at the variation of simulation time for every value of the actual driving time one could also try to create a model involving just the means and medians of the simulation time per actual time value (which yields even better results!).

The data

structure(list(actual = c(120, 60, 120, 120, 240, 60, 120, 180, 
120, 60, 180, 420, 420, 180, 300, 240, 60, 180, 180, 60, 300, 
180, 240, 180, 60, 180, 420, 240, 60, 360, 180, 60, 240, 180, 
60, 60, 780, 60, 180, 240, 480, 240, 180, 120, 660, 180, 60, 
300, 420, 180, 240, 360, 840, 180, 240, 600, 300, 120, 60, 180, 
120, 60, 60, 120, 60, 180, 180, 180, 120, 360, 300, 180, 60, 
180, 360, 180, 180, 180, 180, 180, 240, 300, 600, 60, 60, 180, 
180, 600, 300, 60, 120, 300, 180, 60, 120, 60, 120, 120, 180, 
120, 120, 120, 240, 120, 120, 600, 120, 120, 180, 360, 300, 240, 
60, 180, 120, 420, 120, 180, 60, 120, 180, 240, 360, 300, 240, 
120, 180, 180, 300, 240, 180, 120, 180, 120, 120, 120, 240, 120, 
180, 180, 180, 60, 120, 180, 120, 420, 60, 180, 180, 240, 180, 
300, 180, 180, 360, 240, 540, 240, 120, 60, 120, 120, 60, 60, 
180, 180, 60, 180, 360, 300, 180, 240, 180, 180, 120, 120, 180, 
60, 180, 180, 240, 240, 180, 180, 180, 180, 180, 240, 120, 180, 
120, 180), simulation = c(194.28940773, 212.275300026, 220.287079812, 
24.607690572, 407.197437288, 81.217067244, 24.607690572, 150.680236818, 
478.658294676, 136.179299352, 377.049865722, 194.28940773, 261.164245608, 
319.750185012, 220.287079812, 351.498241422, 8.703469632, 478.658294676, 
24.607690572, 173.848915098, 220.287079812, 81.217067244, 212.275300026, 
24.607690572, 136.179299352, 150.680236818, 220.287079812, 407.197437288, 
377.049865722, 204.83267784, 220.287079812, 173.848915098, 220.287079812, 
212.275300026, 136.179299352, 194.28940773, 351.498241422, 377.049865722, 
478.658294676, 407.197437288, 664.460391996, 659.49136734, 171.987490656, 
162.42626667, 485.496425628, 360.000858306, 121.588454244, 24.607690572, 
478.658294676, 171.987490656, 152.808523176, 664.460391996, 659.49136734, 
360.000858306, 485.496425628, 162.42626667, 24.607690572, 274.938783648, 
121.588454244, 115.878911016, 385.97213745, 94.89244938, 140.229663846, 
262.36567497, 94.89244938, 115.878911016, 115.878911016, 115.878911016, 
239.758086204, 303.008880618, 519.334259034, 68.913009168, 239.758086204, 
353.441877366, 303.008880618, 68.913009168, 68.913009168, 303.008880618, 
280.39235115, 428.468284608, 259.42299843, 182.360544204, 671.648883822, 
96.808075902, 96.598634718, 186.045684816, 369.657411576, 293.113288878, 
392.484369276, 56.862205266, 343.983478548, 369.657411576, 428.468284608, 
80.855455398, 144.722843172, 60.819990636, 157.677226068, 139.932003024, 
78.863933088, 212.355537414, 158.009676936, 243.857574462, 292.072420122, 
167.319359778, 158.009676936, 270.116386416, 158.009676936, 100.485241416, 
349.8108387, 194.206109046, 538.366470336, 174.882373812, 97.03774452, 
428.468284608, 20.02849281, 615.891094206, 169.016976354, 100.77576399, 
158.009676936, 78.04938555, 99.34376478, 226.997423172, 490.142440794, 
88.538596632, 243.464784624, 266.780548098, 212.355537414, 206.20563984, 
343.983478548, 428.468284608, 428.468284608, 158.009676936, 186.045684816, 
144.722843172, 157.677226068, 212.355537414, 428.468284608, 428.468284608, 
210.082454682, 243.857574462, 280.39235115, 96.808075902, 20.02849281, 
369.657411576, 169.016976354, 490.142440794, 80.855455398, 266.780548098, 
428.468284608, 226.997423172, 158.009676936, 343.983478548, 343.983478548, 
243.857574462, 490.142440794, 428.468284608, 671.648883822, 428.468284608, 
428.468284608, 169.016976354, 139.932003024, 78.863933088, 60.819990636, 
96.598634718, 99.34376478, 369.657411576, 80.855455398, 167.319359778, 
194.206109046, 369.657411576, 158.009676936, 212.355537414, 169.016976354, 
186.045684816, 210.082454682, 428.468284608, 144.722843172, 157.677226068, 
212.355537414, 158.009676936, 194.206109046, 158.009676936, 243.857574462, 
428.468284608, 428.468284608, 99.34376478, 428.468284608, 538.366470336, 
280.39235115, 164.87254143, 177.99147606, 99.029567244)), .Names = c("actual", 
"simulation"), row.names = c(NA, -192L), class = "data.frame")

It seems to me that questions one and two are quite distinct, which makes this post rather broad. In this kind of Q&A site, questions with a tight technical focus tend to fare best. I think you might do better to focus on one of the two points - your first question seems more urgent, since you are wondering whether your entire analysis is invalidated by your choices here. You can always ask a follow-up question about linearity, but that question is probably well-covered here already (I suggest you use the site search feature). — Silverfish, Mar 16 '16 at 11:33
Since the GIS is perfectly capable of accounting for any speeds you care to specify along the road segments, why not use it directly to estimate ambulance driving times? — whuber, Mar 16 '16 at 14:38
I think the question is much better now. Thanks for taking the time to edit it. — Silverfish, Mar 16 '16 at 15:58
@whuber The reason why I chose this approach over changing the network segment speeds are the following: 1) I would have to determine real driving speeds for each road type and segment, wich is much harder to do with the given data. The data provides start- and end-points as well as the time the vehicle needed for the trip. 2) The GIS provides quite well working standard driving models that I do not like to change in terms of how vehicles behave on the network. — fr3d-5, Mar 16 '16 at 18:10
Going about the problem indirectly certainly won't overcome the first difficulty; it only ignores it and is doomed to produce an inferior solution. (2) looks irrelevant to me: you need to use a model and data that are appropriate to your problem. The GIS will work just fine using such data. — whuber, Mar 16 '16 at 19:17

score 3 · Accepted Answer · edited Apr 13 '17 at 12:44

No, I don't believe you should force the regression through zero. Nor do I believe that your argument that an ambulance will always be faster than a simulated normal car holds. Finally, your assertion that "reducing the amount of data will often yield better results" is not correct.

I would argue that your measured actual values have substantial associated uncertainties, since they are (i) measured and (ii) rounded to minutes. That would suggest that you should consider using a regression technique that does not assume zero error in the x-values. Thus, I suggest giving Deming regression a try.

plot(simulation ~ actual, data = DF, xlim = c(0, 850))

fit <- lm(simulation ~ actual, data = DF)
abline(fit, col = "red")

fit1 <- lm(simulation ~ actual - 1, data = DF)
abline(fit1, col = "green")

library(deming)
fit2 <- deming(simulation ~ actual, data = DF, stdpat = c(1,0,1,0))
abline(coef(fit2), col = "blue")

abline(0, 1, lty = 2)

legend("bottomright", legend = c("OLS", "OLS through origin","Deming"), 
       lty = 1, col = c("red", "green","blue"))

Note how the Deming regression gives a result that is even more different from the OLS with intercept than the OLS without intercept.

If you had actual uncertainty estimates for each point (or at least for each variable), you could improve the model further (see help("deming")).

Finally, it looks a bit like there are actually two relationships behind the data, one creating a steeper slope and one creating a less steep slope. That would be worth investigating: maybe night/day difference? rush hour? weather? ...

Since your goal seems to be prediction: Don't forget to validate your regression model with an independent dataset. (Or at least cross-validate.)

Thanks for the elaborate answer. Some questions: 1) The post regarding regression through zero actually seems to strengthen my point. The prediction for 0 seconds of driving time should be 0 seconds of simulated driving time, right? 2) I too had the impression that the data might have more than one relevant relationship. Maybe larger distances cancel out the advantage of the faster way of traveling. However, I would have to collect more information. 3) Do I get your point right that reducing the data (in terms of using simulation > actual only, or just mean or median data) is a bad idea? — fr3d-5, Mar 16 '16 at 18:28
1) You don't appear to have read the whole post. 2) Good models need good information. You should also consider @whuber's remarks. 3) Using less data might give you models that *appear* to be better, but they will perform worse for prediction. — Roland, Mar 17 '16 at 07:50
Ok, I'll sure go through the post again and I totally agree on the other points. However, since this is the data I have for now and given the idea I was following, your answer put me on the right track. In addition, the comments will help me and other readers to dive deeper into improvement options. — fr3d-5, Mar 17 '16 at 11:55