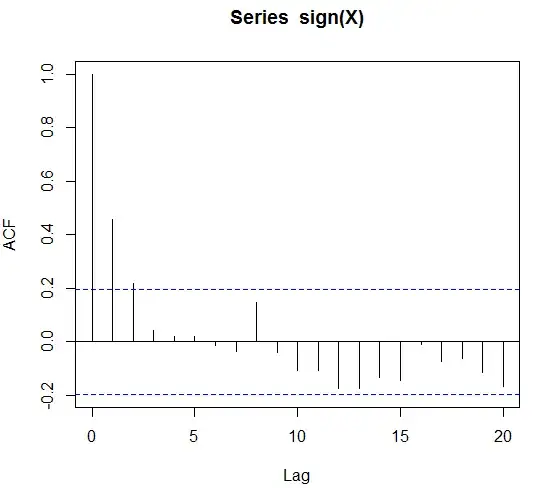
What are the usual approach to modelling binary time series? Is there a paper or a text book where this is treated? I think of a binary process with strong auto-correlation. Something like the sign of an AR(1) process starting at zero. Say $X_0 = 0$ and $$ X_{t+1} = \beta_1 X_t + \epsilon_t, $$ with white noise $\epsilon_t$. Then the binary time series $(Y_t)_{t \ge 0}$ defined by $$ Y_t = \text{sign}(X_t) $$ will show autocorrelation, which I would like to illustrate with the following code
set.seed(1)
X = rep(0,100)
beta = 0.9
sigma = 0.1
for(i in 1:(length(X)-1)){
X[i+1] =beta*X[i] + rnorm(1,sd=sigma)
}
acf(X)
acf(sign(X))
What is the text book/usual modelling approach if I get the binary data $Y_t$ and all I know is that there is significant autocorrelation?
I thought that in case of external regressors or seasonal dummies given I can do a logistic regression. But what is the pure time-series approach?
EDIT: to be precise let's assume that sign(X) is autocorrelated for up to 4 lags. Would this be a Markov model of order 4 and can we do fitting and forecasting with it?
EDIT 2: In the meanwhile I stumbled upon time series glms. These are glms where the explanatory variables are lagged observations and external regressors. However it seems that this is done for Poisson and negative binomial distributed counts. I could approximate the Bernoullis using a Poisson distribution. I just wonder whether there is no clear text book approach to this.
EDIT 3: bounty expires ... any ideas?