5

I'm cross-posting this from math.SE because it's not getting any love over there. However, if that's considered heresy, I can delete the posting over there.

The Statement of the Problem:

Let $ \{ U_i \}$ be a set (sequence?) of iid random variables such that $U_i \sim \text{Uniform}(0,1)$, and define

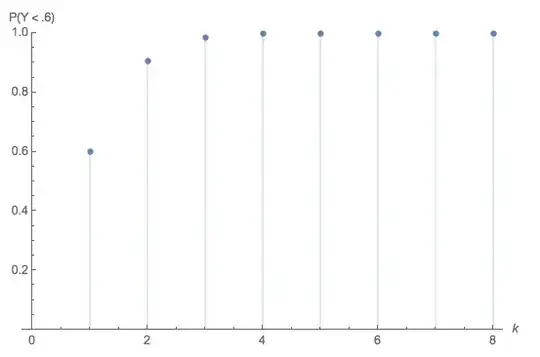
$$ N(a) = \min \left\{k: \prod_{i = 1}^{k}U_i \lt .6\right\}. $$

Find the distribution of $N$.

SOLUTION

Recall that $-\log (U) \sim \text{Expo}(1)$. From this, it follows that

$$N(a) = \min \left\{k: \prod_{i = 1}^{k}U_i \lt .6\right\} = \min \left\{k: \sum_{i = 1}^{k} \left[ - \log ( U_i ) \right] \gt \log \left( \frac{5}{3} \right) \right\} = \min \left\{k: S_k \gt \log \left( \frac{5}{3} \right) \right\} $$

where $S_k$ is the arrival time of the $k$th event of a Poisson process with rate $\lambda = 1$. I understand all of this. Beyond this point is where I get confused...

Now, it follows (apparently) that the smallest $k$ such that $S_k \gt \log \left( \frac{5}{3} \right)$ is

$$ N\left( \log \left[ \frac{5}{3} \right] \right) + 1 \qquad (*) $$

which is distributed as $\text{Poisson}{ \left( \log \frac{5}{3} \right) } + 1$.

I'm not sure what is meant by this sort of "superscript" parameter here (I'm transcribing this from handwritten notes). As far as I can tell, it's just a normal ol' parameter. Anyway, I have no idea where the result $(*)$ comes from, and have been racking my brain here trying to figure it out. Any assistance would be appreciated.

mpiktas
  • 33,140
  • 5
  • 82
  • 138
thisisourconcerndude
  • 165
  • 6
  • 1
    What you have after "(apparently)" doesn't make sense to me; you're computing $N$, and the answer has an $N$ in it -- so it defines $N$ in terms of $N$. – Glen_b Mar 06 '16 at 20:54
  • Ah. Yes, it's a bit unclear. $N$ is random variable, and so the expression in the brackets is its parameter. I'll try to edit the post to reflect this. – thisisourconcerndude Mar 06 '16 at 20:56
  • I concur with Glen_b, your notations make no sense. – Xi'an Mar 06 '16 at 21:02
  • 1. You should not migrate the post now, you already posted this one. I was explaining what you should have done instead of what you did so you'd know for next time. 2. If you have enough reputation on the original site you'll have the ability to close as off-topic with a migration-option (but if you have that much reputation you should probably already have noticed that option is there). But don't migrate. If you doubt there will be any help there, you're free to delete. – Glen_b Mar 06 '16 at 21:03
  • @Xi'an Well, like I said, I'm transcribing this from handwritten notes, and I'm a bit confused myself about some of this notation -- hence my posting it here. However, I agree that at least one part doesn't make much sense: the definition of $N$ implies that it's parameter would be integer-valued, but then we have it taking $\log (5/3)$? I'll have to get some clarification from the author, I suppose... – thisisourconcerndude Mar 06 '16 at 21:24
  • What does parameter $a$ represent? Why don't you write: Find the distribution of $$ K = \min \left\{k: \prod_{i = 1}^{k}U_i \lt .6\right\}. $$ – wolfies Mar 07 '16 at 03:24
  • The relation between a Poisson process and an exponential distribution is explained in [this answer](http://stats.stackexchange.com/a/2094/7224). – Xi'an Mar 07 '16 at 08:41
  • https://math.stackexchange.com/q/4101406/321264 – StubbornAtom Jun 03 '21 at 14:50

1 Answers1

5

Takings logs both sides is smart. Here, just for fun ... is a more brute force approach ...

Let $X_i \sim \text{Uniform}(0,1)$ be iid, and let $Y = \prod_{i = 1}^{k}X_i$ denote the product of $k$ independent Uniforms. Then, the pdf of $Y$, say $h(y)$, can be shown (I used method of induction) to be:

enter image description here

We seek $P(Y<.6)$. More generally, for parameter $a$, the $P(Y<a)$ is:

enter image description here

where I am using the Prob function from the mathStatica package for Mathematica to automate the nitty-gritties, and Gamma[k,z] is the incomplete gamma function $\Gamma(k,z)=\int _z^{\infty } t^{k-1} e^{-t} d t$.

Here is a plot of the solution $P(Y<.6)$ as a function of $k$:

enter image description here

Given cdf sol above, we can derive the corresponding pmf (in $k$) by evaluating $\text{sol}(k) - \text{sol}(k-1)$, which yields the pmf $f(k)$:

$$f(k) = \frac{a}{(k-1)!} (-\log (a))^{k-1} \quad \text{for } k = 1,2,3, \dots$$

Note that this does indeed have the Poisson form $\frac{e^{-\lambda } \lambda ^x}{x!}$ where $\lambda = -\log (a)$, and $x = k-1$.

Here is a plot of the corresponding pmf $f(k)$ (again when $a = .6$):

enter image description here

wolfies
  • 6,963
  • 1
  • 22
  • 27