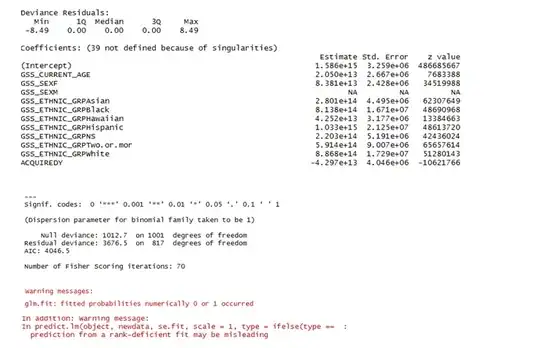
Logistic Regression using R's glm package is giving me the following summary (snap of the few first variables).
My Data Set:
- Dimensions: 1252 rows and 224 columns (after using model.matrix). The Data has been standardized.
- Response variable is binary.
- Trying to predict if an employee will leave the company, based on employee attributes
My Understanding:
The model does not give a good fit because:
- Residual Deviance > Null Deviance.
- p.value = 1 - pchisq(3676.5, 817) turns out to be 0.
- The first warning about 0 or 1 fitted probability message suggests that due to some predictor(s) the model might be giving perfect predictions
- Second warning on ‘rank deficiency’ suggests that there might be predictors that are linearly dependent on one another.
My Questions:
- How can I improve the model? I would like to see Residual Deviance < Null Deviance. I will invest time on dropping the linearly dependent variables in the model, but is there anything I should do first to test the ‘model’ itself, before revisiting my data? I am asking this because SVM worked quite well on the same data set.
- Why do I have such extreme coefficient values?
- Many answers to other posts state that ‘AIC’ is used to compare different
- The summary parameters (coefficients , std error and p-values) for many dummy factors obtained via model.matrix, like GSS_SEXM, is shown as 'NA'. Why is it so?
- logistic models. What is meant by ‘different’ here? Models trained on different data sets that bear different coefficients, like say different set of attributes?