If $N(1,4)$, find $P(X<0)$ and $P(|x|>4)$. I already have the answers which are $0.3085$ and $0.07302$ respectively. please note this is not a homework. Can someone explain in detail how to reach the answer? I tried multiple times but every time I am not getting it.
-
1This thread answers your question: https://stats.stackexchange.com/questions/19195/explaining-two-tailed-tests if for some reason it doesn't, please edit your question to clarify what is not clear. – Tim Feb 22 '16 at 15:26
-
that does not say anything about absolute value ! – user65652 Feb 22 '16 at 15:28
-
Yes it does, absolute value is the same as using two-tailed test. – Tim Feb 22 '16 at 15:31
-
my problem is how to expand the absolute value, usually we have P(1
4)=P(-4>X>4) , it seems very unusual to me. – user65652 Feb 22 '16 at 15:36 -
Given that this is not homework, how did this problem arise? – Glen_b Feb 23 '16 at 10:21
2 Answers
In general case
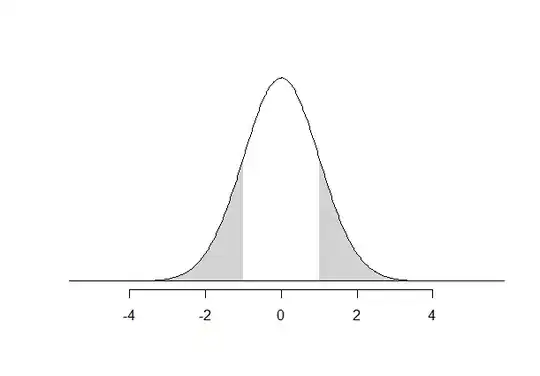
$$ \Pr(|X| > x) = \Pr(X < -x \cup X > x) \\ = \Pr(X < -x) + \Pr(X > x) $$
and since normal distribution is symmetric,
$$ \Pr(X < -x) = \Pr(X > x) $$
what leads to
$$ \Pr(X < -x \cup X > x) = 2 \times \Pr(X > x) $$
You are interested in $\Pr(|X| > x)$ if you want to learn something about tails of distribution, e.g. when you want to learn about probabilities of observing values that are anomalous, outlying, or extreme. If you want to imagine this graphically, we are looking at the two tails of normal distribution (grayed).
You can also easily compute the opposite probability
$$ \Pr(|X| < x) = \Pr(-x < X < x) \\ = \Pr(X < x) - \Pr(X \le -x) \\ = \Pr(X > -x) - \Pr(X \ge x) \\ = 1 - \Pr(X < -x \cup X > x) $$
that is, the "common area" (colored in orange) of the two cases.
Check also a thread about single- vs two-tailed tests that discusses practical application of such interval probabilities.
- 108,699
- 20
- 212
- 390
The 'two tailed' probabilities referred to here Explaining two-tailed tests correspond to the absolute value in your question. P(abs(x)>4) is the same as P(X < - 4) + P (X > 4). Just translate X to a standard Normal variable (subtract the mean and divide by the standard deviation) and look up the corresponding probability.
Or, in R:
For the absolute value one:
pnorm(-4,mean= 1,sd = 2) + (1-pnorm(4,mean = 1,sd = 2))
For the other one:
pnorm(0,mean = 1,sd = 2)
- 520
- 2
- 7
-
we are told that the normal table is only for P(X
4) considering the table I have only takes positive values. ! – user65652 Feb 22 '16 at 15:45 -
can you answer this question in detail ? how does the change in inequality change the answer? – user65652 Feb 22 '16 at 15:46
-
The Normal table is symmetric. If your Normal table is presented as P(X
something) just use 1- P(X – Jordan Collins Feb 22 '16 at 15:54 -
did you ever have a homework which already given you the answer ? I wrote the answer above . – user65652 Feb 22 '16 at 15:56
-
apologies - didn't mean to offend - just looking to see what sort of explanation you were looking for. Tim's answer explains it very well graphically. – Jordan Collins Feb 22 '16 at 16:00
-
No worries, I would like to get complete and detailed answer to P(|x|>4) so I can follow and understand – user65652 Feb 22 '16 at 16:02
-
The complete answer (combined with the Graphs in the answer above) is that P(|X| > 4) = 1 - P(|X| < 4) = 1 - [P(X < 4) + P(X < -4)] – Jordan Collins Feb 22 '16 at 16:05