2

I am trying to convey the results of a Bayesian statistical analysis to an audience uneducated with Bayesian statistics but familiar with the interpretation of p-values (verbal, non-publication setting). The difficulty lies not in interpreting the results, or explaining why a Bayesian analysis was chosen, but in summarizing those results without the need to fully explain the Bayesian process - I am unsure what statements I can accurately make that will best (and most accurately) convey the Bayesian interpretation.

As an example, consider the Bayesian style t-test as described by Kruschke's article Bayesian estimation supersedes the t-test with the following simulated data and a diffuse/uninformative prior. In R: 

set.seed(1)
y1 = rt(50, 5, 5)
y2 = rt(50, 5, 6)
library(BEST)
best = BESTmcmc(y1, y2, numberSavedSteps=10000)
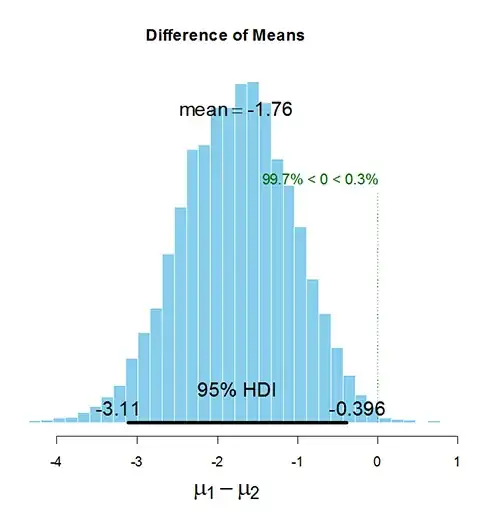
plot(best)

A discrete ROPE value of 0 falls outside the 95% HDI of $\mu$1-$\mu$2, suggesting the group means can be considered credibly different.

enter image description here

  1. How can this be quickly (and accurately) summarized to an audience uneducated in Bayesian statistics without fully explaining Bayesian statistics and its terminology (for example in terms of probability rather than ROPE, HDI, posterior, etc...)?
  2. Is it accurate to extrapolate and report probabilities based upon the credible interval(s)? More generally, is it correct to state that given a discrete ROPE, if X% of the credible interval falls to one side of that ROPE, then there is an X% probability (given the data) that that hypothesis (eg $\mu$1 is less/greater than $\mu$2) is correct? Using the values from the above example, this would read 'give this data, there is a 99.7% probability that the $\mu$1 is smaller than $\mu$2'.
copeg
  • 123
  • 5
  • This is a futile exercise :) I wouldn't even bother explaining anything, just show them the results and tell them it's an alternative way to test hypotheses – Aksakal Feb 18 '16 at 19:32
  • The funniest thing about your example is that your $y_1$ and $y_2$ have the *same mean*, they have differing degrees of freedom which simply change the *scale* of the distribution. So they are different distributions, but their mean is the same. You are confusing strong and weak tests of hypothesis, and this BESTmcmc approach is somewhere in between. Use Kolmogorov Smirnoff for a test of strong null hypotheses, e.g. whether the distributions are different. – AdamO Feb 18 '16 at 20:18
  • Possible duplicate of [what's the advantages of bayesian version of linear regression, logistic regression etc](http://stats.stackexchange.com/questions/43436/whats-the-advantages-of-bayesian-version-of-linear-regression-logistic-regress) – Xi'an Feb 18 '16 at 20:29

2 Answers2

3

Most Bayesian analyses I've encountered don't report the whole posterior, but a summary thereof. A credible interval is a great summary measure that is analogous to the confidence interval that frequentists use. You would need to explain if you've used an informative prior or not. Even we "uneducated" frequentists understand when and why a noninformative prior might be applied.

I would advocate against decision rules, Bayes factors, and all that. The only strength that Bayesian analyses had is that, for a brief, shining, moment, it gave people the notion that "tests" do not really convey significance, but estimation intervals do. Nowhere is this so readily apparent as in two sample tests. And yet the journal of experimental psychology, in their endeavors to defenestrate NHST, have thrown the baby out with the bathwater. Your cited article drives that point home. Even the abstract says "Bayesian estimation for two groups provides...the normality of the data" which is nonsense.

Tests have a contrived interpretation in either context. Just report some CI, any CI, and be done with it.

AdamO
  • 52,330
  • 5
  • 104
  • 209
  • 1
    If all his users are "frequentists" (whatever it means), why does he do Bayesian analysis? My question would be "why are you doing it this way?" if I were a user, there's got to be a reason – Aksakal Feb 18 '16 at 20:10
  • 1
    @Aksakal precisely. I think a lot of confusion arises when people use Bayesian methods to actually obtain exact tests for complex likelihoods, such as, say, a bimodal normal mixture posterior estimate for a mean. I certainly couldn't *write* the likelihood down easily, but an MLE can be estimated with the same MCMC methods that are used to calculate posteriors. That isn't actually a Bayesian method. The OP's example makes the same mistake. – AdamO Feb 18 '16 at 20:16
  • @AdamO, `Tests have a contrived interpretation in either context. Just report...CI...and be done with it.` Great suggestion. Thanks – copeg Feb 18 '16 at 21:24
  • 1
    @copeg I can't take credit for it. Quote is from Casella and Berger, who are also much more qualified than I to make such claims! – AdamO Feb 18 '16 at 21:26
1

For question 1, what I would say if were at your place (while this is obviously an over-simplification, but this is the purpose of the question) is:

  1. Bayesians consider probability as a the representation of the belief of a proposition or event (contrary to frequentist that thinks it as a frequencies of occurence). Consequently, they have no problem in attributing probability to a parameter e.g. the mean of a population $\mu$ or the difference between two means $\mu_1-\mu_2$.

  2. Then given a model and data $x$ they can compute $p(\theta|x)$ that is the belief we have on $\theta$ after having observed $x$ e.g. $p(\mu_1-\mu_2|x,y)$. (Maybe you can add that in some situation designing a well-received model can go with some problems, the prior, but this is the job of the statistician to do it correctly).

  3. When $p(\theta|x)$ is computed, testing weither $\theta$ is lower than $\theta_0$ with a given confidence level can be performed by checking if the region of highest probability of $p(\theta|x)$ covering $1-\alpha$ of the overall density includes or not values $\theta_0>0$ (your graph illustrates this well).

For question 2, I think (but I am not so sure) this is not correct :

if X% of the overall density (and not credible intervals) falls at the right of zero (we do not need any ROPE here), then it is correct to say that there is an X% probability (given the data and model) that hypothesis μ1 is less than μ2 is correct. So if, as you stated, X% of the credible interval falls to one side of that ROPE, then there is at least X% probability (given the data) that that hypothesis (eg μ1 is less/greater than μ2) is correct.

Nevertheless, IMHO hypothesis testing is also a matter of defintion and I see no strong reason to avoid to define that acceptation of hypothesis $\mu_1 < \mu_2$ at a given level using the intersection between the credible intervals associated to $\mu_1-\mu_2 $ and 0.

peuhp
  • 4,622
  • 20
  • 38
  • Just to clarify from @peuhp's comment: Assume we want to test if an intervention X has a positive effect. Are you saying that if we compute the % of the posterior density for the parameter for X which falls to the right of zero then 1 - p(d>0) = p value that the intervention is effective? Does the same apply to combinations of parameters, e.g. p(X1+X2 > 0)? – bjw Jun 07 '17 at 10:21