0

Background:

I try to estimate the potential energy supply within a geographical area using spatially explicit data.

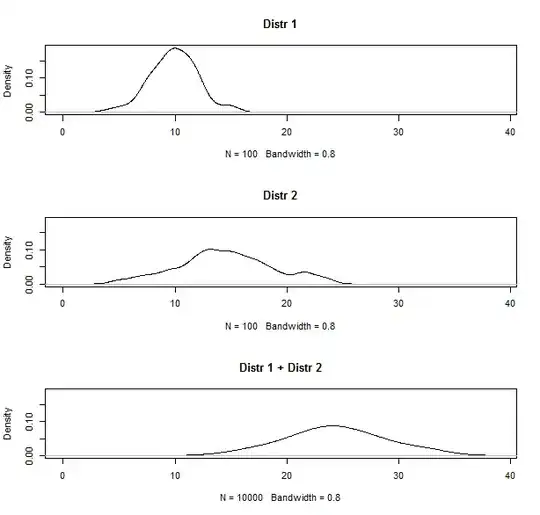
For this purpose I use a Bayesian network and several spatial data layers as input data (e.g resource supply, conversion efficiency). The study area is devided into smaller area entities. For each entity my Bayesian network model reads the input data and computes the corresponding energy supply (MCMC simulations). As a result I obtain for each entity a probability distribution of the expected energy supply (e.g Distr or Distr 2).

However, I am equally interested in the total supply within the study area. That means I need to aggregate (sum) the potential energy supply of all the individual entities in order to get the overall supply potential within the area (e.g. Distr 3).

Question:

I would like to combine several probability distributions by adding their values into one single probability distribution (see above).

  • What is the correct mathematical/statistical term of the operation I want to do?

Below I provide a graphical explanation of what I would like to do.

simplyfied, graphical explanation

Bushroot
  • 101
  • 5
  • 1
    As far as I can see, you want to know how to find the distribution of X+Y, given the distributions of X and Y? If this is the case then you are looking for **convolution** and your question is a duplicate of others on this site, and the background about JAGS is irrelevant. Having said that though, I am puzzled why you would want to sum the distributions you derived in this manner. The R package recommendation question is a software issue which would be regarded as off-topic here. – Silverfish Feb 18 '16 at 15:23
  • Based on the background I wouldn't think this is about convolution - I would have guessed Distr 1 is $p(\theta \mid D_1)$ and distr. 2 is $p(\theta \mid D_2)$ and the OP is looking for $p(\theta \mid D_1,D_2)$. On the other hand, the graphical example looks like a convolution indeed. – Juho Kokkala Feb 18 '16 at 17:38
  • @R.Bushroot can you clarify in what sense you want to 'sum' the distributions - why are you interested in the sum? It might be helpful to explain the background of this question in real-life terms (what is the variable of interest, what is the sum supposed to represent). – Juho Kokkala Feb 18 '16 at 17:39
  • I added some background information in order to clarify in what sense I want to "sum" the distributions and why I want to do that. – Bushroot Feb 22 '16 at 10:23
  • OP accepted an answer stating that the answer is indeed convolution. IMHO, this strengthens the case to close as duplicate. – Sycorax Feb 22 '16 at 14:20
  • If similar questions on stackoverflow count as duplicate, I agree that the question can be closed as duplicate. In contrast, the proposed duplicate "Why does convolution work?" explaines convolotion but does present the question to the anser stated here. – Bushroot Feb 22 '16 at 14:59

1 Answers1

0

The correct term is "convolution"!

As similar question has already been discussed on stackoverflow. Once the term is known, it its not difficult to find further information online (e.g.):

Community
  • 1
Bushroot
  • 101
  • 5